Des suites réelles
Soit la fonction: ![]() On peut définir la suite de termes:
On peut définir la suite de termes: ![]() La définition de la suite est complète si l’on donne son premier terme u0. On peut représenter graphiquement les premiers termes de cette suite.
La définition de la suite est complète si l’on donne son premier terme u0. On peut représenter graphiquement les premiers termes de cette suite.
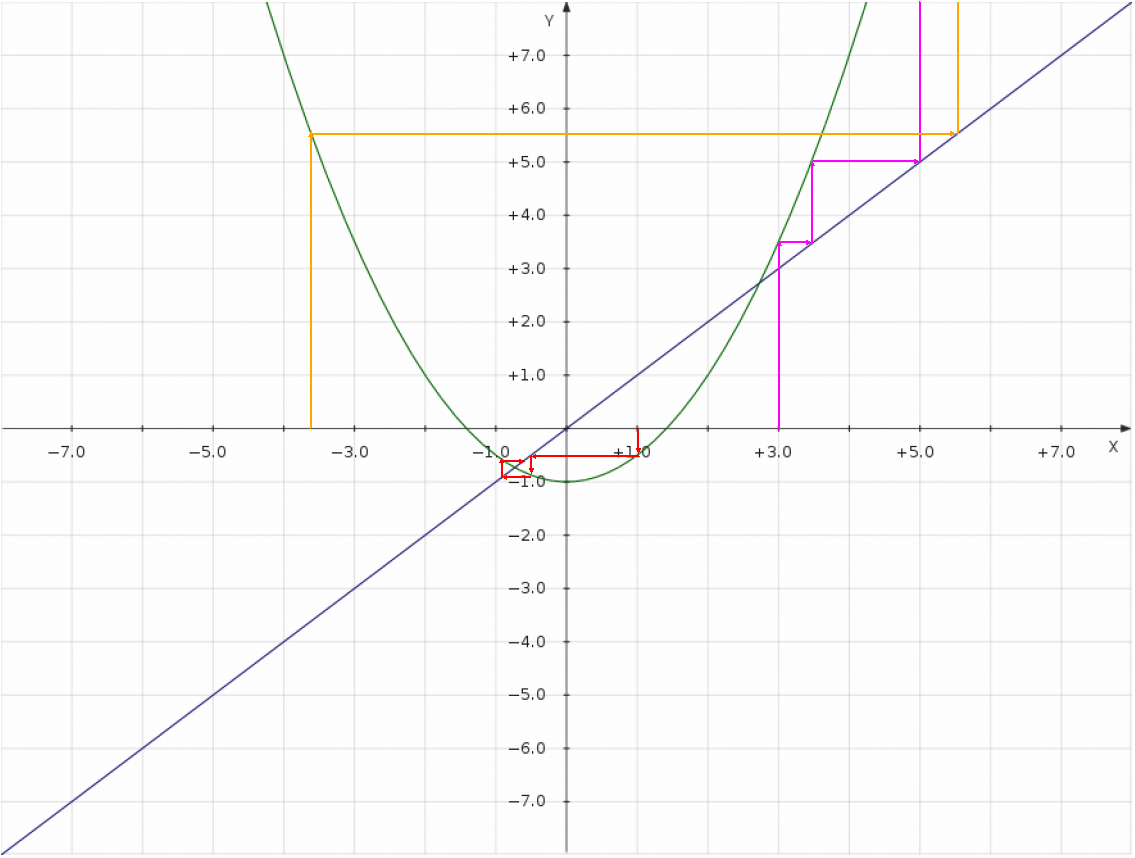
En vert la fonction f. En bleu la droite d’équation y=x qui est un moyen simple et élégant de convertir le résultat de la fonction (d’ordonnée y) en son entrée (d’abscisse x = y) pour calculer le terme suivant. En rouge, magenta et orange, la construction des débuts des suites de premiers termes 1, 3 et -3.6.
On observe qu’il y a alors 2 possibilités: soit la suite construite converge vers un point fixe qui est une valeur vérifiant f(x) = x, soit la suite diverge en tendant vers plus l’infini. On notera qu’il y a deux points fixes: 1 + sqrt(3) et 1 – sqrt(3). Mais aucune suite ne converge vers le premier mis à part celles dont le premier terme est cette valeur ou son opposé ! L’ensemble des nombres réels est ainsi partagé en 3 domaines:
- l’ensemble des nombres donnant des suites convergeant vers 1 + sqrt(3) (contenant deux éléments: 1+sqrt(3) et -1-sqrt(3))
- l’ensemble des nombres donnant des suites convergeant vers 1 – sqrt(3) (c’est l’ensemble ]-1-sqrt(3) , 1+sqrt(3)[)
- l’ensemble des nombres donnant des suites divergeant en tendant vers plus l’infini
A noter que la fonction f n’a rien de particulier. Le même type d’étude peut être fait avec n’importe quelle fonction.
Les mêmes, mais complexes
L’application de ce même raisonnement aux nombres complexes va nous conduire à un domaine captivant.
Si l’on reprend la même fonction et que l’on calcule les premières valeurs des suites pour différentes valeurs de u0, on trouve que certaines sont cycliques (pour 1+i par exemple), que d’autres convergent (0.2+0.7i par exemple) et que d’autres divergent (1+2i par exemple).
Vous pouvez jeter un coup d’oeil au résultat de l’étude de quelques suites sous wxMaxima. Et voici le fichier source correspondant.
Il n’est pas aussi facile que dans le domaine des réels de délimiter les ensembles de point selon le comportement de la suite correspondant. Afin de mieux comprendre ce qui se passe, il semble intéressant de repérer sur le plan complexe, par exemple, les points pour lesquels la suite diverge d’une couleur et ceux pour lesquels elle ne diverge pas d’une autre.
Ensembles de Julia en python
Le résultat que l’on obtient est un ensemble de Julia rempli. L’ensemble de Julia pour un complexe C donné est l’ensemble des points z0 pour lesquels la suite récurrente suivante est bornée (i.e ne diverge pas):
zn = zn-12 + C

Ensemble de Julia pour C=-0.35-0.63125i
À noter que l’ensemble de Julia, contrairement à l’ensemble de Julia rempli, n’est que la frontière des valeurs z0 pour lesquelles la suite est bornée, c’est à dire la frontière de l’ensemble que nous allons tracer.
Concrètement, dans notre programme en python pour savoir si la suite diverge, nous allons calculer ses termes jusqu’à ce qu’ils dépassent en module une certaine valeur ou jusqu’à un nombre maximum d’itérations. Si ce nombre maximum est atteint, nous considérerons que la suite ne diverge pas (ce qui peut être faux au voisinage de l’ensemble, la suite pouvant simplement diverger lentement).
Voici le programme en python permettant de tracer des ensembles de Julia.
Les contrôles suivants sont disponibles:
- R pour choisir aléatoirement une nouvelle valeur de C
- C pour recommencer le tracé
- P pour multiplier par 2 le nombre maximum d’itérations (ne relance pas le tracé du début, ce qui permet d’observer l’impact)
- M pour diviser par 2 le nombre maximum d’itérations (même remarque)
- Clic gauche: zoom d’un facteur 10 autour d’un point
- Clic droit: dezoom d’un facteur 10 autour d’un point
- Echap pour quitter
Le programme étant assez lent, il peut être intéressant de baisser la résolution pour jouer avec et de la réaugmenter si l’on désire de plus belles images.
Essayons par exemple de tracer l’ensemble pour C=0.162-0.574i. Pour cela, modifions la valeur de C dans le programme par C = complex(0.162, -0.574). Nous obtenons, avec la valeur par défaut du nombre maximum d’itérations, un ensemble fractal bien visible. Augmentons le nombre d’itérations à 800 (en appuyant 3 fois sur P) puis retraçons (en appuyant sur C).
Le résultat que nous obtenons est très différent. L’ensemble a presque entièrement disparu ! Il est probable qu’en augmentant encore le nombre maximum d’itérations, il se réduise encore plus. Attention donc à ne pas confondre l’image tracée et la réalité de l’ensemble de Julia …

Un « mirage » de Julia, pour C = 0.162-0.574i qui disparaît lorsque l’on augment le nombre maximum d’itérations.
Un ensemble de Julia très connu est le lapin de Douady, pour C = -0.123+0.745i (ou C = -0.123-0.745i).

Un lapin de Douady, l’ensemble de Julia correspondant à C=-0.123-0.745i
Ensemble de Mandelbrot en python
L’approche pour tracer les ensembles de Julia a été, pour un C donné caractérisant l’ensemble, d’étudier pour chaque point z0 du plan complexe, la divergence de la suite zn = zn-12 + C.
On peut aussi partir d’un z0 donné, typiquement z0 = 0 et étudier pour chaque point C du plan complexe la divergence de cette même suite zn = zn-12 + C.
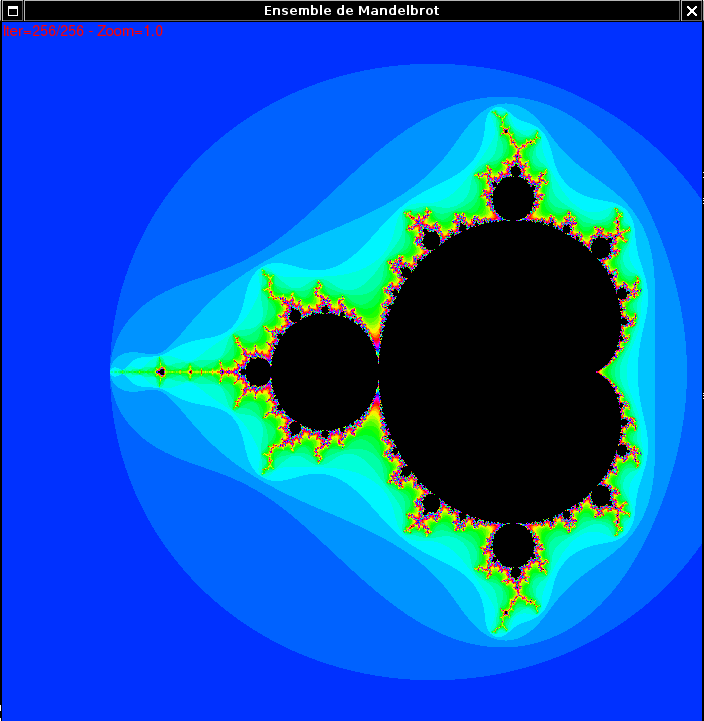
Le résultat obtenu est l’un des objets mathématiques les plus connus: l’ensemble de Mandelbrot.
Voici un programme en python permettant de le tracer. Il est très similaire à celui traçant les ensembles de Julia (c’en est en fait une copie et il serait bien raisonnable de fusionner les deux !).
Les contrôles sont eux aussi inchangés mis à part la touche R qui ne sert plus:
Les contrôles suivants sont disponibles:
- C pour recommencer le tracé
- P pour multiplier par 2 le nombre maximum d’itérations (ne relance pas le tracé du début, ce qui permet d’observer l’impact)
- M pour diviser par 2 le nombre maximum d’itérations (même remarque)
- Clic gauche: zoom d’un facteur 10 autour d’un point
- Clic droit: dezoom d’un facteur 10 autour d’un point
- Echap pour quitter

Ensemble de Mandelbrot
Un ensemble pour les gouverner tous
L’ensemble de Mandelbrot est bien sûr lié aux ensembles de Julia puisque un point C appartenant à l’ensemble de Mandelbrot correspondra à un ensemble de Julia qui contient 0. À l’inverse, un point C n’appartenant pas à l’ensemble de Mandelbrot correspondra à un ensemble de Julia qui ne contient pas 0.
Mais le lien entre l’ensemble de Mandelbrot et les ensembles de Julia est en réalité plus fort que ça. Les points appartenant à l’ensemble de Mandelbrot correspondent aux ensembles de Julia connexes, c’est à dire les ensembles de Julia qui ne se résument pas à des points isolés.
Formulé de manière moins rigoureuse, on peut dire que l’ensemble de Mandelbrot indexe les ensembles de Julia « intéressants », c’est à dire ceux que l’on verra graphiquement.
Voici donc un programme en python juxtaposant l’ensemble de Mandelbrot et un ensemble de Julia. En cliquant sur un point de l’ensemble de Mandelbrot, l’ensemble de Julia correspondant est tracé. Il est possible de zoomer sur l’ensemble de Mandelbrot afin de sélectionner les points de manière plus précise. Le point sélectionné est affiché dans la console, permettant d’avoir sa valeur exacte.
Les contrôles suivants sont disponibles:
- R pour recommencer le tracé
- P pour multiplier par 2 le nombre maximum d’itérations (ne relance pas le tracé du début, ce qui permet d’observer l’impact)
- M pour diviser par 2 le nombre maximum d’itérations (même remarque)
- C pour passer en mode sélection de point (mode par défaut)
- Z pour passer en mode zoom
- D pour passer en mode dezoom
- Clic gauche sur l’ensemble de Mandelbrot: selon le mode, sélectionne un point pour tracer l’ensemble de Julia correspondant, zoom ou dezoom d’un facteur 2 autour d’un point
- Echap pour quitter

Ensemble de Mandelbrot indexant les ensembles de Julia
Acceleration du tracé
Le tracé de ces courbes est assez lent. Pour l’accélérer, nous allons commencer par étudier ce qui prend du temps. Pour cela, nous allons le modifier pour qu’il n’effectue que le tracé puis quitte immédiatement. Nous allons aussi ajouter du code de profilage.
Nous plaçons le code suivant avant le code a profiler:
import cProfile, pstats, StringIO pr = cProfile.Profile() pr.enable()
Et le code suivant après:
pr.disable() s = StringIO.StringIO() sortby = 'cumulative' ps = pstats.Stats(pr, stream=s).sort_stats(sortby) ps.print_stats() print s.getvalue()
Le programme résultant est disponible ici.
Le résultat du profiling est le suivant:
1860144 function calls in 33.857 seconds
Ordered by: cumulative time
ncalls tottime percall cumtime percall filename:lineno(function)
40000 21.817 0.001 31.566 0.001 Mandelbrot1.py:26(converge)
1739140 8.534 0.000 8.534 0.000 {abs}
40000 1.698 0.000 1.698 0.000 {pygame.draw.line}
40200 1.223 0.000 1.223 0.000 {range}
200 0.426 0.002 0.426 0.002 {pygame.display.flip}
1 0.082 0.082 0.082 0.082 {pygame.base.quit}
200 0.034 0.000 0.034 0.000 {method 'render' of 'pygame.font.Font' objects}
201 0.025 0.000 0.025 0.000 {pygame.event.get}
200 0.018 0.000 0.018 0.000 {method 'blit' of 'pygame.Surface' objects}
1 0.000 0.000 0.000 0.000 {method 'fill' of 'pygame.Surface' objects}
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
Nous voyons que la majeure partie du temps est passée à calculer si la suite converge ou non et entre autre dans la fonction abs qui calcule le module.
C’est plutôt rassurant, mais comment améliorer cela ? Une première idée est d’utiliser des nombres réels représentant la partie réelle et la partie imaginaire plutôt que le type complexe de python.
Le programme correspondant est disponible ici.
Le résultat est plutôt bon:
121004 function calls in 19.225 seconds
Ordered by: cumulative time
ncalls tottime percall cumtime percall filename:lineno(function)
40000 15.565 0.000 16.808 0.000 Mandelbrot_reel.py:26(converge)
40000 1.593 0.000 1.593 0.000 {pygame.draw.line}
40200 1.249 0.000 1.249 0.000 {range}
200 0.635 0.003 0.635 0.003 {pygame.display.flip}
1 0.106 0.106 0.106 0.106 {pygame.base.quit}
200 0.032 0.000 0.032 0.000 {method 'render' of 'pygame.font.Font' objects}
201 0.023 0.000 0.023 0.000 {pygame.event.get}
200 0.021 0.000 0.021 0.000 {method 'blit' of 'pygame.Surface' objects}
1 0.000 0.000 0.000 0.000 {method 'fill' of 'pygame.Surface' objects}
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
Nous avons presque divisé le temps de calcul par 2. Mais c’est encore assez lent !
Nous pouvons accélérer considérablement en changeant la façon dont nous avons structuré le programme. Plutôt que de calculer pour chaque point si il converge ou non, nous allons utiliser numpy qui est performant pour effectuer le même calcul sur un grand nombre d’éléments.
Le programme est disponible ici et présente en plus l’avantage de faire apparaître la fractale progressivement mais globalement, ce qui donne une animation très jolie en particulier lorsque le niveau de zoom est élevé et le nombre d’itérations important.
Le résultat du profilage est le suivant:
2050 function calls in 5.615 seconds
Ordered by: cumulative time
ncalls tottime percall cumtime percall filename:lineno(function)
256 4.554 0.018 4.554 0.018 Mandelbrot3.py:38(trf)
256 0.728 0.003 0.728 0.003 {pygame.display.flip}
256 0.107 0.000 0.107 0.000 {pygame._arraysurfarray.blit_array}
1 0.094 0.094 0.094 0.094 {pygame.base.quit}
256 0.049 0.000 0.049 0.000 {method 'render' of 'pygame.font.Font' objects}
256 0.042 0.000 0.042 0.000 {method 'fill' of 'pygame.Surface' objects}
256 0.022 0.000 0.022 0.000 {method 'blit' of 'pygame.Surface' objects}
256 0.014 0.000 0.014 0.000 {pygame.event.get}
256 0.005 0.000 0.005 0.000 {method 'transpose' of 'numpy.ndarray' objects}
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
On remarque que l’affichage, bien qu’encore minoritaire dans le temps consommé, n’est plus tout à fait négligeable.
Si l’on réfléchi à ce que fait notre nouveau programme, on se rend compte qu’il fait de nombreuses opérations inutiles ! Il va effectuer toutes les itérations sur tous les points, contrairement aux programmes précédents qui, pour chaque point, s’arrêtaient dès qu’il était évident que la suite divergeait. Et malgré ça, cette version est plus rapide grâce à numpy.
Mais ne pourrait on pas transposer l’idée de s’arrêter de calculer pour les points dont on sait qu’ils donnent des suites divergentes à cette version du programme ? C’est possible, au prix d’une contorsion rendant le programme un peu plus difficile à comprendre. Pour pouvoir supprimer des points de nos matrices, elles ne doivent plus être à deux dimensions. Nous allons donc construire nos matrices à 2 dimensions puis les aplatir pour enlever petit à petit les points qui sont hors de l’ensemble. Nous devons conserver deux matrices supplémentaires correspondant aux coordonnées des points restant: ce seront les indexes de nos tableau à 1 dimension.
Voici cette version du programme.
Et le résultat est excellent:
2050 function calls in 2.119 seconds
Ordered by: cumulative time
ncalls tottime percall cumtime percall filename:lineno(function)
256 0.969 0.004 0.972 0.004 Mandelbrot4.py:50(trf)
256 0.740 0.003 0.740 0.003 {pygame.display.flip}
256 0.154 0.001 0.154 0.001 {pygame._arraysurfarray.blit_array}
1 0.132 0.132 0.132 0.132 {pygame.base.quit}
256 0.051 0.000 0.051 0.000 {method 'render' of 'pygame.font.Font' objects}
256 0.038 0.000 0.038 0.000 {method 'fill' of 'pygame.Surface' objects}
256 0.021 0.000 0.021 0.000 {method 'blit' of 'pygame.Surface' objects}
256 0.011 0.000 0.011 0.000 {pygame.event.get}
256 0.003 0.000 0.003 0.000 {len}
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
Il est possible cependant d’aller encore un peu plus loin. Pour cela, il faut revenir aux complexes (la différence n’est plus si énorme que ça avec numpy) et utiliser un autre module python: numexpr. Ce module permet de compiler des expressions numériques ce qui permet d’en accélérer l’execution.
On peut de plus gagner encore en compilant une expression qui effectue plusieurs itérations d’un coup. C’est à double tranchant: calculer l’expression une fois sera moins cher que de faire N fois le calcul, mais pas N fois mon cher. On gagnera donc du temps sur les valeurs pour lesquelles on aurait fait N fois le calcul de toute façon, mais comme on éliminera les valeurs pour lesquelles la suite diverge plus tard il peut y’avoir un surcoût. Quelques tests semblent montrer que l’optimal est autour de 6, c’est à dire une expression qui est:
(((((z**2+c)**2+c)**2+c)**2+c)**2+c)**2+c
Cette version du programme est disponible ici.
La sortie du profilage est plus verbeuse à cause de numexpr, mais en voici le début pour vous mettre l’eau à la bouche:
39142 function calls (12830 primitive calls) in 1.214 seconds
Ordered by: cumulative time
ncalls tottime percall cumtime percall filename:lineno(function)
43 0.121 0.003 0.942 0.022 Mandelbrot5.py:51(trf)
43 0.166 0.004 0.734 0.017 /usr/lib/python2.7/site-packages/numexpr/necompiler.py:662(evaluate)
1 0.000 0.000 0.480 0.480 /usr/lib/python2.7/site-packages/numexpr/necompiler.py:534(NumExpr)
1 0.001 0.001 0.477 0.477 /usr/lib/python2.7/site-packages/numexpr/necompiler.py:481(precompile)
9185/301 0.124 0.000 0.256 0.001 /usr/lib/python2.7/site-packages/numexpr/necompiler.py:80(__hash__)
9185/301 0.132 0.000 0.252 0.001 {hash}
1 0.012 0.012 0.241 0.241 /usr/lib/python2.7/site-packages/numexpr/necompiler.py:322(collapseDuplicateSubtrees)
1 0.002 0.002 0.130 0.130 /usr/lib/python2.7/site-packages/numexpr/necompiler.py:343(optimizeTemporariesAllocation)
43 0.105 0.002 0.105 0.002 {pygame.display.flip}
1 0.100 0.100 0.100 0.100 {pygame.base.quit}
79 0.086 0.001 0.086 0.001 {abs}
Ce qu’il faut noter ici, c’est qu’une grosse partie du temps est passée dans la compilation de l’expression, qui n’est effectuée qu’une seule fois. Donc si l’on refait nos tests avec une résolution plus élevée, le gain sera encore plus important.
Version artistique
Vous aviez sans doute déjà vu l’ensemble de Mandelbrot, et même si il ressemblait vaguement à nos tracés, dans vos souvenir, il était haut en couleurs, avec des spirales et des formes variées. Pourquoi n’est-ce pas le cas ici ?
Nous avons utilisé deux couleurs: du bleu pour les points n’appartenant pas à l’ensemble et du noir pour les points appartenant à l’ensemble (ou pour ceux pour lesquels nous n’avons pas encore pu déterminer qu’il n’en faisaient pas parti car ils faut un nombre d’itérations supérieur au maximum que nous nous sommes fixés pour s’en rendre compte).
Mais nous pouvons, comme nous l’avons fait dans les premiers exemples, utiliser une couleur qui reflète le nombre d’itérations qu’il faut à la suite correspondant à un point pour que son module dépasse 2 (seuil qui nous permet de dire qu’elle diverge). En utilisant une palette plus complexe que celle utilisée (qui était un simple dégradé du bleu vers le rouge) nous obtenons de belles images.
Mais ce n’est pas seulement de l’art: ces couleurs contiennent une information. Elle représentent les différents éléments de la suite d’ensemble qui converge vers l’ensemble de Mandelbrot.

Zoom sur l’ensemble de Mandelbrot en couleurs
Comment choisir une bonne palette de couleurs ? Il y a au moins deux règles qui semblent intéressantes:
- Que deux couleurs successives soient proches, afin de former un dégradé
- Qu’aucune couleur ne soit proche du noir, afin de ne pas confondre les points appartenant à l’ensemble et ceux n’en faisant pas partie
Pour obtenir cela, nous partons d’une couleur pure, par exemple le bleu (#0000FF). Nous allons incrémenter la composante verte jusqu’à arriver à du cyan (#00FFFF). A partir de là nous allons décrémenter la composante bleu jusqu’à arriver à du vert (#00FF00). Nous poursuivons la même logique jusqu’à revenir au bleu. La séquence de couleurs obtenue est la palette de transition progressive entre les extrêmes suivants:
- #0000FF (bleu)
- #00FFFF (cyan)
- #00FF00 (vert)
- #FFFF00 (jaune)
- #FF0000 (rouge)
- #FF00FF (magenta)
- #0000FF (bleu)
- etc …
Afin que les couleurs soient visibles dès le niveau de zoom le plus bas, on ne va pas utiliser toutes les couleurs de notre palettes une par une (il y en a 1531) mais seulement une sur 3 ou 4 environ.
A noter que si l’on veut marquer chaque itération, il faut mettre iterDepth à 1 (c’est à dire désactiver l’optimisation qui consiste à calculer plusieurs valeurs successives de la suite à chaque itération). On peut aussi augmenter vitesseCouleur afin de mieux distinguer les étapes successives.
Ensemble de Mandelbrot en couleurs marquées (iterDepth = 0 et vitesseCouleurs = 50). On voit bien en particulier le cercle de rayon 2 centré à l’origine au delà duquel les suites divergent dès le premier élément.
Vous pouvez télécharger cette version colorée du programme ici.
Les contrôles suivants sont disponibles:
- R pour recommencer le tracé
- F pour accentuer l’écart entre les couleurs successives de la palette
- S pour diminuer l’écart entre les couleurs successives de la palette
- P pour multiplier par 2 le nombre maximum d’itérations (ne relance pas le tracé du début, ce qui permet d’observer l’impact)
- M pour diviser par 2 le nombre maximum d’itérations (même remarque)
- Clic gauche sur l’ensemble de Mandelbrot: zoom autour du point cliqué
- Clic droit sur l’ensemble de Mandelbrot: dezoom en centrant sur le point cliqué
- Echap pour quitter
N’hésitez pas à partager vos améliorations et vos plus belles captures dans les commentaires !
Variations
Au delà des ensembles que nous avons vu, il est facile d’en découvrir de nouveau en faisant varier l’équation servant à définir la suite. Ainsi, en faisant varier l’exposant, en rajoutant un facteur ou en utilisant un polynôme plus complexe, on fait apparaître de nouvelles fractales. Ces variations sont possibles aussi bien en partant des ensembles de Julia que des ensembles de Mandelbrot.

Un ensemble de Julia coloré
Essayez donc les équations suivantes (n, m, p et q étant des constantes à fixer):
- n*z**2 + C
- n*z**m + C
- n*z**m + p*z**q + C
- etc …

Ensemble semblable à celui de Mandelbrot pour z^4 + C. On observe 3 « bulbes »
Voici un programme permettant de faire ces tests pour des polynomes de degré inférieur ou égal à 12, aussi bien pour les ensembles similaires à ceux de Julia que pour ceux similaires à ceux de Mandelbrot.
Les contrôles suivants sont disponibles:
- J – trace l’ensemble « de Julia »
- M – trace l’ensemble « de Mandelbrot »
- V – diminue l’écart entre les couleurs successives de la palette
- Shift + V – augmente l’écart entre les couleurs successives de la palette
- F1 à F12 – sélectionne le coefficient du polynôme à modifier
- PAGE UP – augmente la valeur du coefficient sélectionné
- PAGE DOWN – diminue la valeur du coefficient sélectionné
- A – diminue la partie réelle de C pour un ensemble de type Julia
- Shift + A – augmente la partie réelle de C pour un ensemble de type Julia
- B – diminue la partie imaginaire de C pour un ensemble de type Julia
- Shift + B – augmente la partie imaginaire de C pour un ensemble de type Julia
- I – diminue le nombre maximum d’itérations
- Shift + I – augmente le nombre maximum d’itérations
- Clic gauche sur l’ensemble: zoom autour du point cliqué
- Clic droit sur l’ensemble: dezoom en centrant sur le point cliqué
- Echap pour quitter

Ensemble semblable à celui de Mandelbrot pour z^10 + C. On observe 9 « bulbes ». D’une manière générale, pour z^n + C on observera n-1 bulbes.
Pour aller plus loin:
Wikipedia:
http://fr.wikipedia.org/wiki/Ensemble_de_Julia http://fr.wikipedia.org/wiki/Lapin_de_Douady http://fr.wikipedia.org/wiki/Ensemble_de_Mandelbrot
Open Classrooms:
http://fr.openclassrooms.com/informatique/cours/dessiner-la-fractale-de-mandelbrot
Le chapitre 6 du film « Dimensions » traite des fractales (les autres chapitres méritent aussi d’être regardés !):
http://www.dimensions-math.org/Download_Lyon.htm
Etude mathématique:
http://maths.wikidot.com/iteration-d-une-fonction-complexe
http://maths.wikidot.com/mandelbrot-et-julia
Informations sur numpy:
http://math.mad.free.fr/depot/numpy/essai.html http://dakarlug.org/pat/scientifique/html/numpy.html
http://mathprepa.fr/?dl_name=www.mathprepa.fr-une-petite-reference-numpy.pdf
