Qui est-ce qui sait ce que c’est que le Qui-est-ce ?
« Qui-est-ce? » (en anglais « Guess who ? ») est un jeu de société bien connu qui se joue à deux et qui s’adresse plutôt aux jeunes enfants. Chaque joueur a devant lui un plateau contenant 24 portraits et pioche une carte correspondant à un des portraits. Le but est d’être le premier à deviner la carte piochée par l’autre joueur en posant une série de questions fermées (dont la réponse est soit oui soit non).
Par exemple:
– Est-ce que ton personnage a les yeux bleus ?
– Oui (Le joueur peut coucher tous les portraits n’ayant pas les yeux bleus)
– Est-ce que c’est une femme ?
– Non (Le joueur peut coucher tous les portraits de femme)
Lorsque l’on y joue, il pourrait sembler que la chance est prépondérante pour gagner: tomber sur une caractéristique rare du personnage (femme -la parité n’étant pas respectée par le jeu !-, roux, yeux bleu) permettant d’éliminer beaucoup de portraits alors que tomber sur une caractéristique qu’il n’a pas ne permet d’en éliminer que peu.
Mais si la chance permet de gagner une partie à toute vitesse, son effet devrait s’estomper et s’équilibrer entre les joueurs au fil des parties. Or dans les règles originales de l’édition française, le premier arrivé à 5 victoires est le gagnant. Alors, une fois l’effet de la chance atténué, existe-t-il une stratégie gagnante ?
Considérations mathématiques
Dans la suite, on appellera « réponse positive » la réponse permettant d’éliminer le plus de portraits. Une réponse positive peut donc correspondre à « oui » ou « non » selon la façon dont la question est posée (yeux bleus / yeux marrons) et selon le contexte (24 portraits dont 5 avec les yeux bleus en début de partie ou 3 portraits dont 2 avec les yeux bleus à la fin d’une partie donnée).
Plus une caractéristique est rare, plus une réponse positive permet d’éliminer de portraits. Une caractéristique rare semble donc un bon choix. Mais d’un autre côté, en poussant ce raisonnement à l’extrême, autant demander tout le temps « Est-ce que ton personnage est Max ? »: si la réponse est positive on a gagné en une question ! Mais la réponse a peu de chance d’être positive … Pour être précis, elle a une chance sur 24.
En réalité, il y a même une chance sur 23 puisque vous savez que le personnage de l’adversaire est différent du vôtre. Cependant, pour simplifier, on ne tiendra pas compte du personnage tiré par le joueur lui même et considérerons donc 24 personnages « candidats » pour la première question.
Les mathématiques nous offrent un outil pour faire le choix le plus rationnel en présence d’événement probabiliste: l’espérance mathématique. C’est la valeur moyenne d’une grandeur si l’on considère tous les scenarii possibles en tenant compte de leur probabilité. Par exemple, lorsque je demande si le personnage est Max, j’ai 1 chance sur 24 de tomber juste et d’éliminer 23 personnages. Mais j’ai aussi 23 chances sur 24 de mal tomber et d’éliminer seulement 1 personnage.
L’espérance du nombre de personnages éliminés X en posant la question « est-ce Max ? » est:
E(X, Max) = 1/24 * 23 + 23/24 * 1 ≈ 1,9
Si on pose cette question au début de chaque partie, en moyenne sur un grand nombre de parties, elle aura éliminé 1,9 portrait par partie. Ce n’est pas beaucoup ! En comparaison, la question sur les yeux bleus permet d’éliminer au moins 5 joueurs (réponse négative) avec une probabilité de 19/24. En cas de réponse positive (probabilité de 5/24), elle élimine 19 joueurs. Quelle espérance cela nous donne ?
E(X, Yeux bleus) = 19/24 * 5 + 5/24 * 19 = 7.9
Il vaut donc bien mieux commencer par la question « A-t-il les yeux bleus ? » que « Est-ce Max ? », ce qu’on savait déjà intuitivement.
Qu’en est-il des autres options de questions ? On constate que l’espérance ne dépend que d’une variable: la fréquence de la caractéristique considérée. Si N personnages possèdent une caractéristique, l’espérance correspondante est:
E(X, N) = 2*N*(24-N)/24
En traçant cette courbe, on s’aperçoit que la valeur optimale est N = 12. Il est assez facile de retrouver ce maximum en étudiant la fonction elle même qui est une simple équation du second degré (la courbe tracée est donc une parabole) dont le coefficient de poids le plus fort est négatif (-1/12) et dont la dérivée -N/6+2 s’annule pour N/6 = 2 soit N = 12.
Cette étude se généralise facilement aux cas où il reste non pas 24 mais un nombre arbitraire M de portraits. La meilleure question est toujours celle pour laquelle la cardinalité de réponses positive (resp. négatives) est le plus proche de M/2.
La situation est similaire à la recherche dichotomique où, sauf connaissance préalable sur la répartition des données, le plus efficace est de comparer l’élément du milieu de l’intervalle dans lequel on recherche.
On peut aussi approcher le problème à l’aide de la théorie de l’information qui associe une grandeur, l’information, à chaque réponse possible. L’information contenue dans une réponse est lié à la réduction d’incertitude qu’elle permet. Dans notre cas, lorsqu’une réponse contient beaucoup d’information la réponse « opposée » en contient peu et ce que l’on cherche à maximiser est l’information moyenne souvent notée H:
En pratique
Malheureusement, il n’existe pas de caractéristique permettant d’éliminer systématiquement la moitié des portraits (homme/femme serait un bon candidat dans un jeu paritaire !). Il nous faut donc trouver la ou les questions s’en rapprochant le plus. Pour cela, on peut dresser une liste des personnages et de leurs caractéristiques. La première version de la liste se concentrant sur les caractéristiques « évidentes » est peu concluante, la cardinalité variant entre 4 et 6. Bien sûr, préférer les questions ayant une cardinalité de 6 augmente la probabilité de victoire mais on préférerait une différence plus marquée !
En creusant un peu, on peut cependant trouver des caractéristiques plus efficaces comme les fossettes (7) ou les rides sur le front (8). Le problème est que ces questions sont moins tranchées que les autres: il faudra peut être les compléter en précisant si l’on considère que Alex a une fossette ou que Frans a des rides sur le front.
Voici un tableau récapitulatif au format ODS (Open Document Spreadsheet) et la version au format CSV.
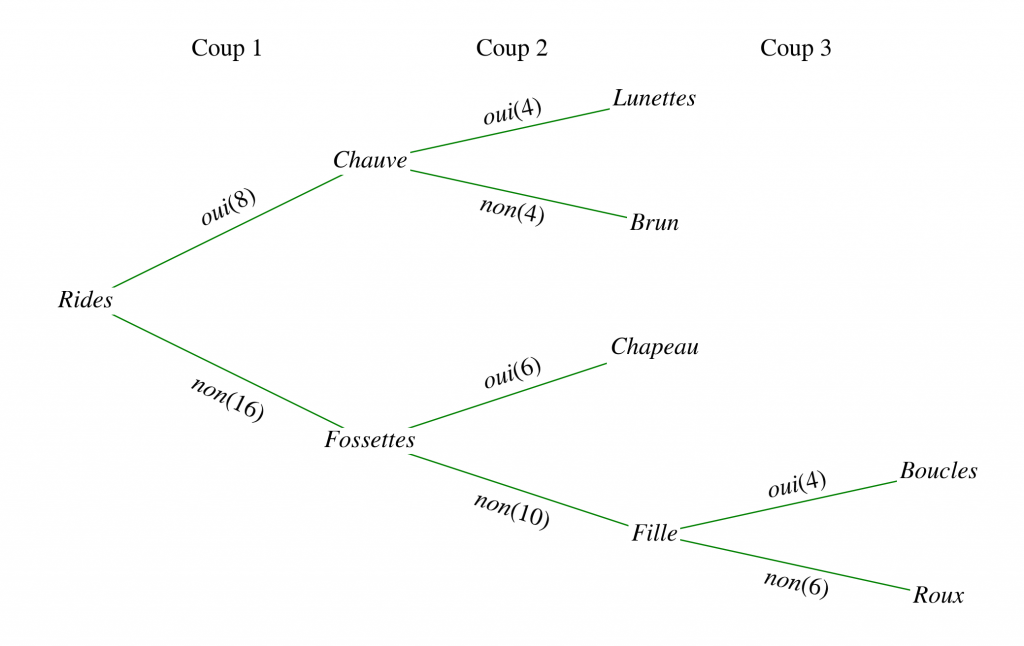
Une bonne option pour la première question à poser est « A-t-il des rides ? », qui permet d’éliminer soit 8 soit 16 portraits. Bien sûr, en fonction de la réponse, les proportions changent et la seconde question à poser peut varier. Si la réponse est oui, une bonne option est de demander en suite « Est-il chauve ? ». Si la réponse est non, la question « A-t-il une fossette ? » est plus adaptée. Cette ouverture permet de jouer assez bien, les questions suivantes étant plus simples à trouver.
Voici de manière plus détaillée l’arbre d’ouverture que je propose:
Il permet de gagner, dans le pire des cas, en 6 questions, les cardinalités successives étant alors 24, 16, 10, 6, 3, 2 puis 1. Une recherche dichotomique dans un ensemble de 24 éléments permettrait, elle, d’obtenir la solution en 5 coups au maximum, les cardinalités successives étant 24, 12, 6, 3, 2 puis 1.
Pour les plus rusés, une approche dichotomique est possible mais elle pourrait être considérée comme une forme de tricherie, ou tout au moins un sacré détournement des règles. Avez-vous une idée ?
Variantes à 2 cartes
La règle du jeu propose, pour les joueurs les plus forts, une variante à 2 cartes. Le principe est simple: au lieu de piocher 1 carte, chaque joueur pioche 2 cartes. Il faut alors poser des questions de la forme: « Est-ce que l’un des deux personnages au moins a les yeux bleus ? ». La règle ne précise pas si l’on peut distinguer les personnages et poser des questions du type « Est-ce que le personnage qui a des lunettes a aussi les yeux bleus ? ». On considérera que non.
Quelle différence cela fait-il pour nous ? Avec cette contrainte, une réponse positive n’est plus une bonne chose ! En effet, si l’on sait qu’un des deux personnages a les yeux bleus, on ne peut éliminer ni les yeux bleus ni les yeux marrons.
A noter que la couleur des cheveux nous offre à première vue un angle d’attaque intéressant: deux questions successives garantissent d’éliminer des personnages: soit l’une des réponses au moins est négative et l’on peut éliminer la couleur correspondante, soit les deux réponses sont positives et l’on peut éliminer toutes les autres couleurs.
Autre différence: la probabilité d’une réponse positive (que l’on cherche maintenant à éviter) a augmenté. Avec une carte, il y a 5 chances sur 24 que le personnage ait les yeux bleus, soit un probabilité de 0,21. Avec deux cartes, la probabilité d’une réponse positive devient:
p(bleus) = 1 – p(2 marrons) = 1 – (19/24 x 18/23) = 0,38
On a donc environ 2 chances sur 3 seulement d’éliminer des portraits en posant cette question.
Avec une caractéristique plus rare, comme les boucles d’oreilles, la probabilité augmente, on a environ 3 chances sur 4 d’éliminer des portraits:
p(boucles) = 1 – p(2 sans boucle) = 1 – (21/24 x 20/23) = 0,24
Mais bien sûr, on en élimine moins ! Il faut donc en revenir à l’espérance pour savoir quelle est la meilleur stratégie. Pour une caractéristique possédée par N personnes, l’espérance d’élimination est maintenant:
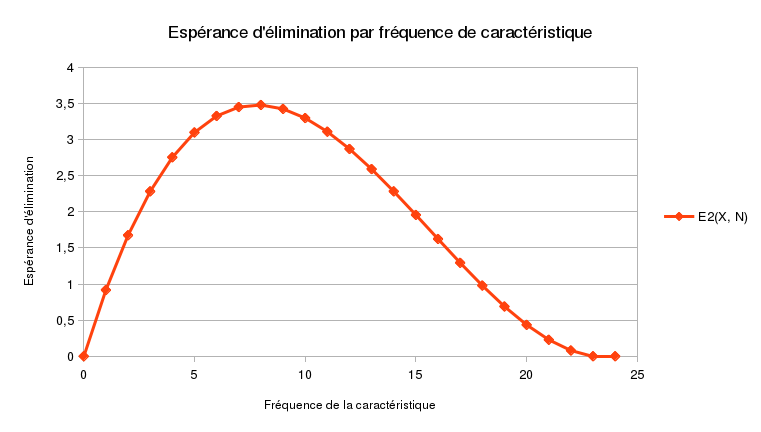
E2(X, N) = N(24-N)(23-N)/(24×23)
Il n’y a plus qu’un seul terme car la réponse positive n’élimine aucun portrait. La réponse négative élimine N portraits. La probabilité qu’elle se produise est le produit de (24-N)/24 et de (23-N)/23 qui sont les probabilités de tirer un premier personnage, puis un second, tous deux sans la caractéristique choisie. Le résultat est un polynôme du troisième degré dont voici le graphe:
On voit qu’une stratégie permettant d’éliminer 3,5 portraits par coup en moyenne peut être considérée comme assez bonne ! Si l’on compare à la stratégie de la couleur des cheveux, dans le pire des cas, on élimine 14 personnages en 5 questions ce qui représente une moyenne de 2,8 portraits par coup. Dans la majeure partie des cas, on éliminera en fait 14 personnages en 3 ou 4 coups, soit 3,5 ou 4,7 portraits par coup en moyenne. Ce semble donc être une bonne stratégie pour commencer la partie !
Cependant, ces considérations ne tiennent pas compte de l’information qu’une question peut nous fournir plus tard dans la partie, en étant combinée à d’autre. Cette approche est intéressante et fait travailler les neurones. Je me propose de faire travailler votre ordinateur à la place !
En fait, l’approche optimale est la même que pour le jeu normal mis à part qu’il ne faut plus considérer l’ensemble des personnages mais l’ensemble des paires de personnages. Cet ensemble ne comporte plus 24 éléments mais 24×23/2 = 276 éléments (la formule venant du fait qu’on a 24 choix pour le premier personnage, 23 pour le second mais il faut diviser par deux car chaque paire peut être piochée de deux manière: soit dans un ordre soit dans l’autre).
Ce programme en python permet de calculer les fréquences en se basant sur le fichier CSV disponible plus haut. Il produit la sortie suivante:
276 couples Non à 'Sourcils bruns' permet de supprimer 153 paires (55.4%) avec une probabilité de 44.57% Non à 'Couettes' permet de supprimer 253 paires (91.7%) avec une probabilité de 8.33% Non à 'Grosses Levres' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Rides au front' permet de supprimer 120 paires (43.5%) avec une probabilité de 56.52% Non à 'Frisés' permet de supprimer 153 paires (55.4%) avec une probabilité de 44.57% Non à 'Moustache' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Roux' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Longs' permet de supprimer 190 paires (68.8%) avec une probabilité de 31.16% Non à 'Blonds' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Blancs' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Chapeau' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Chatains' permet de supprimer 190 paires (68.8%) avec une probabilité de 31.16% Non à 'Fossette' permet de supprimer 136 paires (49.3%) avec une probabilité de 50.72% Non à 'Gros Nez' permet de supprimer 153 paires (55.4%) avec une probabilité de 44.57% Non à 'Yeux Bleus' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Lunettes' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Femme' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Chauve' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Bruns' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Boucles d'oreilles' permet de supprimer 210 paires (76.1%) avec une probabilité de 23.91% Non à 'Pomettes rouges' permet de supprimer 171 paires (62.0%) avec une probabilité de 38.04% Non à 'Barbe' permet de supprimer 190 paires (68.8%) avec une probabilité de 31.16%
On voit que la première question la plus intéressante est ‘Un des personnages a-t-il une fossette ?’ qui nous permet d’éliminer près de la moitié des possibilités, quelle que soit la réponse. En modifiant légèrement le programme pour filtrer les couples à considérer en fonction des réponses aux questions précédentes, on trouve facilement la meilleure question à chaque étape. Il faut 9 questions pour trouver à coup sûr les 2 personnages en utilisant cette méthode.
Par rapport à la stratégie des couleurs de cheveux, on se retrouve avec moins de 10 paires possibles après 5 coups joués contre 25 (5 personnages possibles pour la première couleur de cheveux, 5 pour la seconde). Cette méthode dichotomique est donc plus efficace dans le cas le pire. Cependant, elle est très stable (les proportions sont toujours très proche de 50%). Dans le cas le plus favorable, commencer par les couleurs de cheveux permet de se retrouver à 25 paires au second coup ce qui est imbattable. Qu’en est-il en terme d’espérance ?
Les probabilités de trouver les deux couleurs de cheveux en N coups sont environ (en considérant autant de personnages de chaque couleur de cheveux, ce qui est presque valide):
- 1/10 en 2 coups
- 2/10 en 3 coups
- 3/10 en 4 coups
- 4/10 en 5 coups
Pour une esperance approximative de nombre de coups de:
E = 2×1/10 + 3×2/10 + 4×3/10 + 5×4/10 = 4
Soit 4 coups en moyenne. Avec l’approximation d’une répartition égale des couleurs de cheveux, on se retrouve donc à 25 candidats après 4 coups pour l’approche « couleur de cheveux » contre 20 candidats après 4 coups pour l’approche dichotomique.
C’était en fait prévisible ! Quand on y pense, l’approche dichotomique inclue l’approche des couleur de cheveux. Se restreindre à la couleur des cheveux est une simplification plus abordable pour le cerveau humain mais qui fournit une moins bonne séparation des candidats. Le mieux que l’on puisse faire, avec une question fermée et des candidats équi-distribués, est d’en éliminer la moitié. Toute question permettant d’en éliminer plus le fera avec une probabilité trop faible pour être avantageuse.
Dernières considérations à prendre en compte pour jouer parfaitement au « Qui-est-ce ? » à deux cartes: éliminer ses propres personnages des couples. Cela réduit le nombre de couples candidats à 231 et le nombre de coups nécessaires pour gagner à 8. Voici un programme implémentant cette approche. Avec quelques imperfections tout de même:
- il ne sait pas, en l’état, poser de questions comme « Un personnage a-t-il les yeux marrons » qui est l’opposé des yeux bleus à une carte mais ne l’est plus à deux cartes !. Mais c’est une lacune facile à combler.
- il ne sait pas poser de questions du types « Les deux personnages ont-il la même couleur de cheveux ? » qui pourraient être meilleures dans certains cas.
- il n’explore pas les conséquences d’une question: une question peut être aussi bonne qu’une autre en terme d’espérance d’élimination immédiate mais aboutir systématiquement à un résultat où la question suivante sera mauvaise.
- il ne sait pas exploiter le reflet dans le miroir situé derrière l’adversaire pour « deviner » ses cartes !
Pour aller plus loin
https://fr.wikipedia.org/wiki/Qui_est-ce_?
https://fr.wikipedia.org/wiki/Espérance_mathématique
https://fr.wikipedia.org/wiki/Dichotomie



Merci pour cet article, qui m’a confirmé que mes calculs étaient bons, les présente de manière plus claire que je ne l’aurais fait et m’a permis de rebondir et creuser dessus (cf l’article que j’ai pu publier du coup) !
Il y existe en faite plein de façon d’avoir un critère N=12, on peut poser des questions avec des « ou » pour interroger sur plusieurs critères à la fois. Exemple, « ton personnage a t’il un chapeau ou les yeux bleus ?
C’est une question parfaitement légale car c’est une question en Oui ou non .
Sinon, la technique théorique la plus simple pour éliminer la moitié des personnage potentiel à chaque coup, est une question du genre, « est-ce-que ton personnage fait partie de cette liste: (là vous listez la moitié des personnages potentiels) ».
Effectivement, on peut combiner plusieurs caractéristiques ou lister les personnages. Une version plus simple de cette dernière option est « ton personnage est il avant tel nom dans l’ordre alphabétique ? » qui permet une approche dichotomique en utilisant la liste de tous les personnages dans l’ordre alphabétique.
Bonjour,
Savez-vous si il existe un algorithme permettant de générer un jeu qui est-ce selon X critères ?
Je souhaite faire un jeu avec les membres de ma famille. Je voulais me faire un petit programme javascript qui me générerait les combinaisons à proposer. J’avais défini 4 critères : sexe, génération, chapeau, lunettes (voir un 5ème critère « grimace »). J’étais partie pour faire en sorte qu’aucune de ces combinaisons n’existe 2 fois. Et je commençais à faire du 50-50.
Par exemple « il y a autant d’hommes que de femmes, et il y a autant d’homme que de femme dans chaque génération, et il y a autant d’homme à chapeau que de femme à chapeau dans une même génération » etc…
Je me suis rendue compte que ce n’était pas la meilleure chose à faire car globalement à chaque question on supprimerait la moitié des cartes restantes.
Mais du coup je ne sais pas quelle proportion attribuer à chaque critère pour que le jeu reste intéressant.
Je me dis qu’il doit forcément exister un algo quelque part qui selon le nombre de cartes, de critères, et de complexité voulus, générera les combinaisons à faire.
En avez-vous entendu parlé ?
Bonne journée,
Aude
Effectivement, la parité au qui-est-ce casse un peu le jeu 🙂
Je ne sais pas quelle logique ont suivi les créateurs du qui-est-ce, mais j’ai l’impression qu’ils ont donné un avantage aux critères les moins évidents (rides, fossette). Dans votre cas, vous partez sur quelques critères évidents donc cette partie est sans doute à oublier.
S’assurer qu’il n’y ait aucune combinaison qui n’existe deux fois est effectivement important si l’on veut pouvoir finir le jeu.
Pour la répartition, en re-regardant le tableau CSV/ODS de l’article, je ne vois rien de spécial, les personnages ayant tous entre 0 et 5 caractéristiques, la majeure partie ayant 3 ou 4. Ça ressemble vraiment à une répartition aléatoire.
Dans votre cas, l’algorithme (pas très original) que j’adopterais est donc le suivant (pour 24 personnages):
– Prendre 4 ou 5 hommes et 20 ou 19 femmes (ou l’inverse [1])
– Prendre à peu près autant de personnes de chaque génération [2]
– Puis répartir les chapeau, lunettes et grimaces un peu au hasard de manière à respecter le critère d’unicité
[1] Ou meme si vous avez 48 membres de la famille, pourquoi ne pas faire deux versions avec des répartitions différentes pour nécessiter différentes stratégies 🙂
[2] Idéalement il faut au moins 5 générations et prendre au maximum 5 de chaque. En pratique ça risque d’être dur, et du coup la génération risque de devenir le choix évident … À noter qu’une répartition inégale est aussi intéressante (par exemple 1, 3, 4, 5, 5, 6 avec 6 générations)
Si vous découvrez des choses intéressantes, que vous avez d’autres idées autour du jeu et/ou si vous avez un résultat à partager, ça m’intéresse! L’idée me parait vraiment excellente.
Merci pour cet article très intéressant qui permet de voir le jeu « Qui est-ce ? » sous l’angle toujours utile des probabilités mathématiques. Je m’étais d’ailleurs demandé pourquoi le jeu était sexiste, il est évident que la question H/F deviendrait trop évidente si tel était le cas…
Oui, les version récentes (comme celle que mes enfants ont) ont corrigé cette inégalité, mais du coup toutes les parties commencent par « Est-ce un garçon/une fille? » (après 2 ou 3 parties, le temps qu’ils le réalisent).
Après tout, d’un point de vue pédagogique, c’est peut être mieux. Ça rend plus évident le fait qu’une question proche du 50/50 est plus efficace …