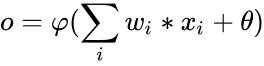Un algorithme miracle
Ces dernières années, les progrès des ordinateurs ont été fulgurants dans de nombreux domaines dans lesquels ils étaient auparavant lamentables: reconnaissance d’image, synthèse vocale, jeu de go, traduction, voitures autonomes etc … Tous ces résultats impressionnants reposent sur l’utilisation d’une même famille d’algorithmes: les réseaux de neurones.
Cet algorithme n’a rien de compliqué. Comment un algorithme simple peut résoudre des problèmes aussi compliqués ? Son secret est de s’appuyer sur une grande quantité de données et d’en extraire des informations, qui idéalement, résument ce que l’on souhaite faire faire au réseau de neurone.
Pour utiliser un réseau de neurone, il ne faut donc pas simplement le programmer, mais aussi l’entraîner. Cet entrainement nécessite des données (en grands nombre) qui vont être utilisées par un algorithme appelé ‘retro-propagation’ pour calculer les paramètres qui permettront au réseau de neurones d’effectuer la tâche désirée.
Cette information est encodée sous forme de ‘poids’ et de ‘seuils’ (aussi appelés ‘biais’) associés à chaque neurone.
Principe de fonctionnement
Neurone artificiel
L’élément de base constituant un réseau de neurones artificiels est … un neurone artificiel ! C’est simplement une fonction qui prend un certain nombre N de valeurs numériques en entrées (N étant le nombre de neurones dans la couche précédente) et qui fournit une valeur en sortie. Un poids wi est associé à chaque entrée (i est le numéro de l’entrée). Le neurone a aussi un seuil θ (theta, souvent aussi noté b, pour biais) et une fonction d’activation φ (phi) qui est généralement la même pour tous les neurones du réseau

Principe de fonctionnement d’un neurone artificiel ayant n entrées. Image par Chrislb, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=674150
La sortie du neurone est calculée en multipliant chaque valeur d’entrée par le poids correspondant, en y ajoutant le biais et en appliquant la fonction d’activation:
La fonction d’activation φ joue un rôle important: c’est le seul élément non linéaire dans le réseau de neurone. Les fonctions d’activations les plus utilisées sont tanh (tangente hyperbolique), la fonction logistique (ou une autre sigmoïde) ou encore Relu (qui vaut 0 pour x < 0, x pour x >= 0). Cette dernière est de plus en plus utilisée car elle a l’avantage d’être peu gourmande en calculs. Chaque fonction a des avantages et des inconvénients. D’un autre côté, comme nous le verrons dans nos test, son choix n’est pas très important du moment qu’elle n’est pas linéaire (ce résultat est fourni par des résultats de recherche, nos tests limités sur un exemple particulier n’ayant que peu de poids pour appuyer cette affirmation !)
Réseau de neurones
Un réseau de neurones est obtenu simplement en connectant plusieurs couches de neurones entre elles. Le réseau prend des données en entrée. Ces données sont un certain nombre de valeurs numériques. Une première couche ‘cachée’ de neurones est connectée à toutes les entrées. C’est à dire que chaque neurone de la couche va avoir en entrée toutes les données d’entrée du réseau.
Cette couche peut être suivie par d’autres couches cachées. Chaque neurone de chaque couche prendra en entrée les sorties de tous les neurones de la couche précédente. Enfin, une couche de neurones de sortie est connectée à la dernière couche cachée. Les sorties de cette couche constituent la sortie du réseau de neurone.
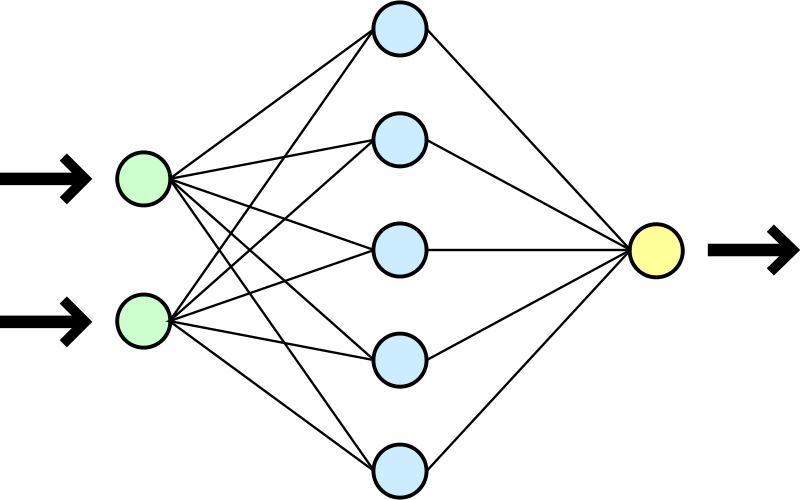
Architecture simplifiée d’un réseau de neurone: les données sont lues par des entrées (en vert) qui sont connectées à une couche de neurones ‘cachés’ (en bleu) qui sont eux-même connectés à une couche de neurones de sortie (en jaune) dont les sorties sont la sortie du réseau de neurones. Un réseau peut avoir plusieurs couches cachées. Image par Dake, Mysid [CC BY 1.0 (https://creativecommons.org/licenses/by/1.0)], via Wikimedia Commons
Différentes architectures
Il existe différentes architectures de réseau de neurones, permettant d’obtenir diverses propriétés. Il est par exemple possible d’avoir des neurones qui court-circuitent certaines couches, ou des neurones dont la sortie est connectée à l’entrée d’une couche précédente (réseaux de neurones récurrents). Dans cet article, nous nous contenteront des réseaux de neurones simples comme ceux décrits jusque là.
Apprentissage supervisé, classification
Il existe de nombreuses manières d’utiliser un réseau de neurone. Dans cet article, nous allons nous intéresser à un seul cas: une classification en apprentissage supervisé. La classification consiste à prédire un label associé à chaque exemple fourni en entrée du réseau de neurone. Par exemple, dire si un animal sur une photo est un chien, un chat, un cheval … Le réseau de neurone a alors un neurone de sortie correspondant à chaque classe et l’idée est d’activer ce neurone lorsque l’entrée correspond à cette classe et de le désactiver sinon. L’apprentissage supervisé consiste à fournir au réseau de neurones des exemples accompagnés de la sortie que l’on attend pour eux (par opposition avec l’apprentissage non supervisé où l’algorithme doit découvrir les classes à prévoir).
Retro-propagation
Au vu de la description ci-dessus, l’implémentation du réseau de neurone devrait être triviale. La partie complexe est l’algorithme de retro-propagation qui permet de calculer les poids et biais à utiliser, c’est à dire d’apprendre.
L’objectif de l’algorithme va être de minimiser l’erreur de notre réseau de neurone. Pour cela, nous allons appliquer notre réseau de neurone à un exemple dont nous connaissons la sortie désirée et calculer l’erreur (typiquement |résultat attendu – résultat obtenu|, ou |x| représente la valeur absolue de x). L’objectif de la retro-propagation va être de minimiser cette erreur.
Le principe théorique sur lequel repose cet algorithme est la descente de gradient. L’idée est de chercher le minimum d’une fonction de plusieurs variables. On part d’un point choisi au hasard et l’on « suit la plus grande pente », c’est à dire la direction pointée par le gradient. La taille du pas que l’on fait est un choix arbitraire mais sera en général proportionnelle au gradient (en tout cas la taille du pas doit tendre vers 0 quand le gradient tend vers 0). Dans des conditions favorables (fonction continuement dérivable, variations « lentes » par rapport à la taille de pas choisie) cet algorithme convergera vers un point où le gradient est nul, ce qui peut être soit un maximum local, soit un point selle, soit un minimum local.
Le premier cas (maximum local) est très improbable, il ne peut se produire que si on le choisit comme premier point ou si l’on tombe dessus à un moment donné à cause d’une taille de pas trop grande. Le point selle par contre n’est pas rare lorsque le nombre de dimensions (c’est à dire le nombre de variables que prend la fonction) est élevé, ce qui est toujours le cas dans les réseaux de neurones en pratique. À noter que même si l’on tombe sur un minimum, ce ne sera le plus souvent qu’un minimum local.
Une solution simple pour éviter de trouver un minimum trop mauvais est de réitérer la descente de gradient plusieurs fois et de garder le meilleur résultat. Cependant, en grande dimension, pour une fonction continue (et même de classe C∞) quelconque, il est très improbable de trouver un très bon minimum et l’on se contentera donc du meilleur point selle/minimum que l’on trouve.
Pour un réseau de neurone, les variables en question sont les poids et biais du réseau de neurone et la fonction est celle qui leur associe l’erreur du réseau de neurone. Dans notre cas, où nous voudrons reconnaître des images de 28×28 en noir et blanc, nous aurons 784 entrées. Si l’on choisit une seule couche de 20 neurones cachés et 10 neurones de sortie (nous verrons plus loin pourquoi), nous avons un total de 784*20 + 20*10 = 15880 poids et 784 + 20 + 10 = 814 biais. Notre réseau de neurones à donc 16694 variables.
Si vous avez du mal à imaginer une descente de gradient en 16694 dimensions, suivez le conseil d’un sage mathématicien anonyme: « imaginez le en N dimensions et posez N = 16694 ».
Le problème d’un si grand nombre de variables, c’est qu’il faut un grand nombre d’exemples pour que le réseau de neurone puisse généraliser son apprentissage. Dans le cas contraire, il peut « se contenter » d’apprendre à reconnaître les exemples sans pour autant être capable de reconnaître de nouveaux exemples. C’est ce qu’on appelle le surapprentissage.
Un exemple classique: reconnaître des chiffres (MNIST)
Il existe de nombreux ensembles de données disponibles publiquement pour évaluer et comparer les différents algorithmes d’apprentissage automatique (machine learning). La base de données de chiffres manuscrits MNIST est très tôt devenu une référence en la matière et reste intéressante, même si elle est maintenant un peu dépassée (les meilleurs algorithmes faisant mieux que les humains avec des taux d’erreurs de moins de 0.3%, d’autres exercices comme la reconnaissance d’images deviennent plus intéressants).
Les données sont disponibles à l’adresse suivante: http://yann.lecun.com/exdb/mnist/
Charger les données
Le format de fichier y est décrit. Le décoder en python est trivial:
import struct
LABELS_FILE_MAGIC = 2049
IMAGES_FILE_MAGIC = 2051
def read_labels(filename, limit=None):
with open(filename, 'rb') as f:
magic = struct.unpack('>i', f.read(4))[0]
if magic != LABELS_FILE_MAGIC:
raise RuntimeError(
"Invalid file type for labels: %s, expected %s"
% (magic, LABELS_FILE_MAGIC))
nb_labels = struct.unpack('>i', f.read(4))[0]
if limit:
nb_labels = min(limit, nb_labels)
result = [struct.unpack('B', f.read(1))[0]
for i in range(0, nb_labels)]
return result
def read_images(filename, limit=None):
with open(filename, 'rb') as f:
magic = struct.unpack('>i', f.read(4))[0]
if magic != IMAGES_FILE_MAGIC:
raise RuntimeError(
"Invalid file type for images: %s, expected %s"
% (magic, IMAGES_FILE_MAGIC))
nb_images = struct.unpack('>i', f.read(4))[0]
if limit:
nb_images = min(limit, nb_images)
nb_rows = struct.unpack('>i', f.read(4))[0]
nb_columns = struct.unpack('>i', f.read(4))[0]
result = []
for i in range(0, nb_images):
pixels = [struct.unpack('B', f.read(1))[0]/255.0
for k in range(0, nb_rows*nb_columns)]
result.append(pixels)
return result
La première méthode lit un fichier contenant les labels et retourne une liste de labels, c’est à dire le chiffre contenu dans une image. La deuxième lit un fichier contenant les images (chaque image faisant 28×28 et étant en niveaux de gris). La valeur des pixels est normalisée entre 0 et 1 (la valeur initiale étant un entier entre 0 et 255). Bien sûr, les deux fichiers sont dans le même ordre afin de savoir quel label correspond à quel image !
Jeter un coup d’œil aux données
Il est toujours sympa de pouvoir jeter un coup d’œil aux données. Dans notre cas, on peut fournir une visualisation rapide en console car les images sont de petite taille et en niveau de gris avec le plus souvent des valeurs extrêmes (blanc ou noir). On obtient donc un résultat sympathique avec le code suivant:
def show_image(image):
result = ""
for i in range(0, 28):
line = ""
for j in range(0, 28):
if self.pixels[i*self.width+j] < 0.01:
line += " "
elif self.pixels[i*self.width+j] < 0.5:
line += "."
else:
line += "#"
result += line + "\n"
Ce qui nous donne par exemple:
Mais aussi, en cherchant un peu, des exemples beaucoup moins lisibles:
Utiliser les données
L’ensemble de données est composé de 4 fichiers: les labels et les images pour l’entraînement et les labels et les images pour la validation. L’idée est que l’on entraîne l’algorithme de machine learning sur l’ensemble d’entraînement puis qu’on évalue son efficacité sur l’ensemble de validation. Cette séparation n’est pas seulement nécessaire à des fins de recherche (pour comparer ses résultats aux précédents et montrer qu’un algorithme est meilleur qu’un autre) mais aussi lorsque l’on désire entraîner un algorithme pour une utilisation concrète. En effet, l’ensemble de validation est le seul moyen de s’assurer que l’algorithme ne surapprend pas.
En pratique, il est même recommandé d’avoir 3 ensembles différents: l’ensemble d’entraînement qui sert à entraîner l’algorithme. Il ne faut pas s’en servir pour l’évaluer car il pourrait surapprendre par l’intermédiaire des poids et des biais. Nous allons donc évaluer ses performances avec un autre ensemble, l’ensemble de validation, qui n’aura pas d’impact direct sur les poids et les biais. Cependant, dans notre recherche des meilleurs paramètres (architecture, nombre de couches, nombre de neurones par couches, multiples descentes de gradients …) nous allons sélectionner ceux qui fournissent les meilleurs performances sur l’ensemble de validation et ces paramètres là peuvent donc d’une certaine manière, être ajustés à cet ensemble. C’est donc une bonne habitude d’avoir un troisième ensemble qui ne sert qu’une fois le modèle figé afin de l’évaluer: l’ensemble de test.
Cette séparation des ensemble est primordiale et il est important de vérifier qu’elle est bien respectée. Par exemple, lorsque j’ai développé le code pour cet article, j’ai initialement oublié d’intégrer la possibilité d’évaluer un échantillon sans sauvegarder l’erreur pour appliquer la retro-propagation (c’est à dire que je n’avais pas codé le paramètre ‘for_training’ dans le code). Je pensais que les données de test ne servait pas à l’entraînement car je n’appelais pas la méthode de retro-propagation, mais en fait les informations associées étaient stockées et l’appel suivant les utilisait. Sans le savoir, l’entrainement se faisait non seulement sur l’ensemble d’entraînement mais aussi sur l’ensemble de validation. Seul l’ensemble de test permet alors de détecter qu’il y a quelque chose de louche en obtenant un score significativement inférieur à l’ensemble de validation.
Ainsi, même si le fait de ne pas tester avec les données d’apprentissage est le B.A.-BA du machine learning (je le savais pertinemment avant cela), il est facile de faire l’erreur de manière subtile. C’est une source d’erreurs fréquente et récurrente, même chez des personnes expérimentées. La différence est que les personnes expérimentées savent mieux comment le détecter et donc s’en protéger.
Implémentation du réseau de neurone
On cherche ici a écrire une implémentation naïve, faisant appel à un minimum de maths (pas de calcul matriciel) et dans laquelle on puisse comprendre ce que fait chaque partie et facilement intégrer toutes sortes de modifications « pour jouer ». Cette implémentation ne sera donc pas très performante mais suivra de près la description faite ci-dessus.
Évaluation
Implémenter la partie évaluation du réseau de neurone est assez facile. La seule difficulté est qu’on ne peut pas utiliser le code sur de vraies données tant qu’on a pas de retro-propagation (à moins de « tricher » en utilisant les poids et biais venant d’une autre implémentation) et qu’il faut donc tester le code avec des exemples fait à la main.
On commence par implémenter un neurone seul:
class Neuron(object):
def __init__(self, nb_inputs, activation):
self.nb_inputs = nb_inputs
self.weights = [random.uniform(-1, 1)
for i in range(0, nb_inputs)]
self.bias = random.uniform(-1, 1)
self.activation = activation
self.prepare_backprop()
def output(self, previous_layer_values):
result = self.bias
for i in range(0, self.nb_inputs):
result += self.weights[i]*previous_layer_values[i]
return self.activation.value(result)
Puis on regroupe les neurones par couches dans un réseau:
class NeuralNet(object):
def __init__(self, inputs_size, layers_sizes, activation):
self.layers = []
self.activation = activation
previous_size = inputs_size
for size in layers_sizes:
self.layers.append([
Neuron(previous_size, activation, average_gradient)
for i in range(0, size)])
previous_size = size
def evaluate(self, inputs):
result = inputs
for layer in self.layers:
result = [neuron.output(result) for neuron in layer]
return result
def predict(self, example):
scores = self.evaluate(example)
return scores.index(max(scores))
Le code est plutôt simple. Il faut fournir au réseau de neurone une fonction d’activation qui peut, par exemple, ressembler à cela (bien qu’à ce stade, la dérivée ne soit pas utilisée):
class TanH(object):
def value(self, x):
return math.tanh(x)
def derivative(self, x):
th = math.tanh(x)
return 1-th*th
Il peut être utile d’implémenter des fonctions permettant de sauvegarder et charger un réseau de neurone. On pourra créer un réseau de neurone pour notre problème avec le code suivant:
net = Neuralnet(784, [20, 10], TanH())
Et essayer de reconnaître un chiffre avec le code suivant:
net.predict(image)
Cependant, le résultat sera décevant à ce stade !
Rétro-propagation
La retro-propagation nécessite, pour chaque neurone de sortie, de calculer son erreur, puis de calculer la contribution de chaque poids, de chaque entrée et du biais. Les poids et le biais seront modifiés proportionnellement à leur contribution à l’erreur. La contribution de l’entrée sera utilisée comme erreur pour réitérer la procédure avec le neurone dont c’était la sortie. On remonte ainsi de couche en couche, d’où le nom de rétro-propagation.
Pour calculer l’erreur, on considère simplement que l’on attendait 1 pour la sortie correspondant au bon label et 0 pour toutes les autres. Pour calculer la contribution de chaque paramètre à l’erreur, on calcule la dérivée partielle de l’erreur par rapport à ce paramètre.
Voyons d’abord les modifications nécessaires au code pour mémoriser les erreurs à chaque évaluation au niveau d’un neurone:
class Neuron(object):
def __init__(...):
(...)
self.prepare_backprop()
def output(..., for_training):
(...)
if for_training:
# Save some info for per-eval backpropagation
self.last_value = result
self.inp = previous_layer_values
return (...)
def prepare_backprop(self):
# Prepare some info for per-round backpropagation
self.dw = [0]*len(self.weights)
self.da = [0]*len(self.weights)
self.db = 0
self.nb_evals = 0
def per_eval_backprop(self, error, learning_rate=1):
self.nb_evals += 1
delta = 2*error * self.activation.derivative(self.last_value)
self.db += delta*learning_rate
for i in range(0, self.nb_inputs):
self.dw[i] += delta*self.inp[i]*learning_rate
self.da[i] += delta*self.weights[i]
# Error contribution to be propagated to the previous layer
return [self.da[i] for i in range(0, self.nb_inputs)]
def per_round_backprop(self):
self.bias += self.db
for i in range(0, self.nb_inputs):
self.weights[i] += self.dw[i]
self.prepare_backprop()
On peut alors utiliser ce code dans le réseau:
class NeuralNet(object):
(...)
def evaluate(..., for_training=False):
(...)
for layer in self.layers:
result = [neuron.output(result, for_training)
for neuron in layer]
return result
def per_eval_backprop(self, errors, learning_rate=1):
result = errors
for layer in reversed(self.layers):
new_result = None
for r, neuron in zip(result, layer):
contrib = neuron.per_eval_backprop(r, learning_rate)
if new_result is None:
new_result = contrib
else:
new_result = [nr + c
for nr, c in zip(new_result, contrib)]
l = len(layer)
result = [nr/l for nr in new_result]
def per_round_backprop(self):
for layer in self.layers:
for neuron in layer:
neuron.per_round_backprop()
def train(self, training_rounds, samples_per_round,
learning_rate, examples, labels):
nb_examples = len(examples)
nb_classes = len(self.layers[-1])
for i in range(0, training_rounds):
error = 0
for j in range(0, samples_per_round):
k = random.randint(0, nb_examples-1)
result = self.evaluate(examples[k], for_training=True)
expected = [0]*nb_classes
expected[labels[k]] = 1
errors = [e - r for r, e in zip(result, expected)]
self.per_eval_backprop(errors, learning_rate)
error += math.sqrt(sum([x*x for x in errors]))
self.per_round_backprop()
La méthode ‘train’ va effectuer plusieurs rounds d’entrainement en utilisant plusieurs exemples par round. Le paramètre ‘learning_rate’ correspond à la taille de pas dans la descente du gradient. Une valeur élevée permet d’avancer plus vite mais risque de sauter par dessus un minimum ou de tourner autour. Il faut donc déterminer empiriquement, à tâtons, une valeur qui convient.
Utilisation
On peut alors entraîner notre réseau de neurone et tester ses performances. On arrive assez facilement à un réseau qui parvient à reconnaître ~95% des chiffres qui lui sont présentés.
Le code complet (incluant de nombreuses améliorations pour automatiser le test de divers paramètres) est disponible sur github:
https://github.com/ColinPitrat/PythonMisc/tree/master/NeuralNet
Une chose intéressante que l’on peut regarder est quels sont les exemples sur lesquels les prédictions sont mauvaises. Est-ce que ce sont des images sur lesquels on a nous aussi du mal à reconnaître le chiffre ? Dans certains cas oui, mais pas systématiquement.
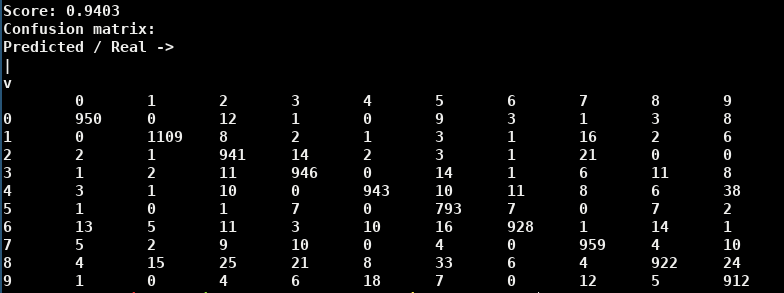
Une autre chose intéressante est de créer une matrice de confusion afin de voir quel chiffre est confondu avec quel chiffre. Une matrice de confusion est simplement un tableau ou chaque ligne correspond à un label prédit et chaque colonne correspond à un label réel. Les cases contiennent le nombre (ou le pourcentage) d’exemples correspondant. Ainsi, les cases de la diagonale donnent le nombre de labels correctement prédits pour chaque valeur.
On voit que les erreurs les plus courantes (seuil arbitraire de 20) sont:
- Un 2 reconnu comme un 8
- Un 3 reconnu comme un 8
- Un 5 reconnu comme un 8
- Un 7 reconnu comme un 2
- Un 9 reconnu comme un 4 ou un 8
Ce réseau de neurones semble avoir tendance à prédire les 8 un (tout petit) peu trop facilement. Des essais avec d’autres réseaux montrent que la confusion 4 <-> 9 est récurrente (ce qui se comprend aisément, il est probable qu’ils correspondent à des chiffres assez mal tracés et vraiment ressemblant) mais que certaines des confusions avec le 8 (en particulier le 5 et le 9) sont accentuées avec ce réseau là.
Ce n’est qu’un début
Il y a encore beaucoup de choses à faire avec ce petit prototype pour mieux comprendre comment fonctionne le réseau, tester des variations dans l’algorithme et l’étendre à d’autres problèmes. Mais ce sera l’objet de prochains articles. D’ici là n’hésitez pas à partager vos trouvailles !
Pour aller plus loin …
Le code complet de l’exemple:
Les données de notre exemple ainsi que des références vers des papiers basés dessus:
Plus de détails sur les concepts que l’on a vu:
- https://fr.wikipedia.org/wiki/Réseau_de_neurones_artificiels
- https://fr.wikipedia.org/wiki/Fonction_d’activation
- https://fr.wikipedia.org/wiki/Algorithme_du_gradient
- https://fr.wikipedia.org/wiki/Fléau_de_la_dimension
- https://fr.wikipedia.org/wiki/Surapprentissage
- https://fr.wikipedia.org/wiki/Matrice_de_confusion
Les réseaux de neurones étant à la mode, bon nombre de youtubers francophones en ont parlé. Entre autres:
Et non francophone mais d’excellente qualité et qui mérite donc d’être regardée si vous parlez un peu anglais: