Que ce soit pour construire des horloges précises, des lignes de chemin de fer confortables ou des grands huit toujours plus impressionnants, la physique à besoin de trouver des courbes présentant des propriétés intéressantes, et de les décrire suffisamment bien pour pouvoir les réaliser.
La courbe éclair
Quel est le chemin le plus rapide entre deux points ? La droite me direz-vous. Et bien non, c’est le chemin le plus court. C’est aussi le chemin le plus rapide si l’on se déplace à vitesse constante. Mais qu’en est-il si la seule source de mouvement est l’accélération de la gravité et que la masse à déplacer a une vitesse initiale nulle ?
Imaginons d’abord que les deux points sont au même niveau. On voit bien que la ligne droite n’est pas une bonne solution: le point ne bougera pas puisque la seule force qui s’exerce sur lui est perpendiculaire au support et donc entièrement compensée par sa réaction ! Alors que la conservation de l’énergie nous dit qu’il est possible de déplacer cette masse, puisqu’en perdant de l’altitude elle peut prendre de la vitesse (conversion d’énergie potentielle en énergie cinétique) qui sera suffisante pour remonter à la même altitude mais à un autre point (conversion de l’énergie cinétique acquise en énergie potentielle).
Une courbe en cloche reliant les deux points par en dessous est donc, dans ce cas précis, meilleur que le segment. Mais quelle est la meilleure courbe ? Et qu’en est-il dans le cas ou les deux points n’ont pas la même altitude (le second étant alors plus bas, la masse ne pouvant pas remonter) ? L’objectif est de trouver l’optimum entre une accélération rapide (découlant d’une forte pente) et la longueur de la courbe.
Ce problème est celui de la courbe brachistochrone et date du XVIIe siècle. La solution est une portion de cycloïde.
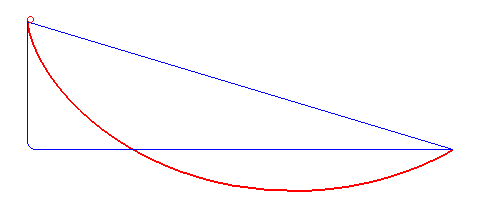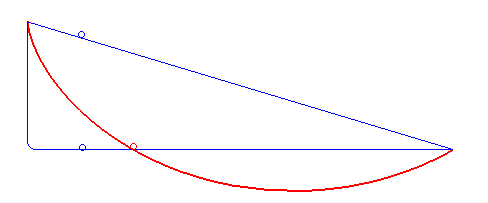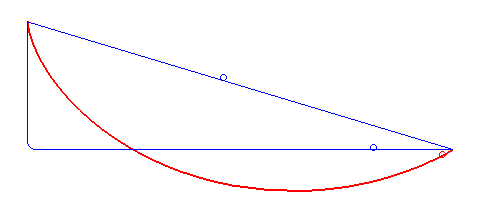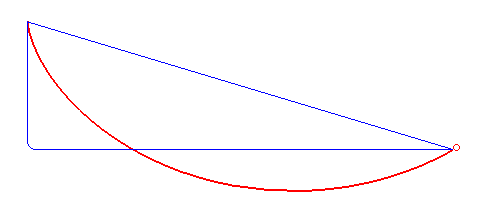
Courbe brachistochrone en rouge. La masse suivant cette trajectoire est plus rapide que toute autre trajectoire reliant les mêmes points de départ et d'arrivée, incluant la ligne droite et la chute libre suivie d'un segment horizontal. (source: Wikipedia)
La courbe horloge
A le doux tic-tac des horloges et de leur pendule qui mesure précisément le temps. Mais un pendule est il vraiment un bon moyen de mesurer le temps ? Sa période n’est en effet pas constante et dépend de l’amplitude avec laquelle il se balance. Existe-t-il une trajectoire qui permettrait d’obtenir des balancement dont la période serait indépendante de l’amplitude ?
Cette question se rapporte à celle similaire que s’est posé, et à laquelle a répondu, Huygens en 1659: trouver la courbe tautochrone, c’est à dire la courbe de la trajectoire sur laquelle une masse soumise à la gravité met un temps T donné pour atteindre le point le plus bas est constante quel que soit le point de départ sur cette courbe. Bien sûr, si la masse part de plus haut, elle arrivera en bas avec une vitesse plus grande.

Courbe tautochrone: toutes les masses arrivent en même temps au point le plus bas, bien qu'elles soient lâchées de positions initiales différentes. (source: Wikipedia)
Afin de transformer cette courbe en pendule, permettant de mesurer le temps de manière régulière, il suffit de la poursuivre par sa symétrique. Une masse placée dans une telle ‘rampe’ oscillera avec une période constante, même si l’amplitude de son mouvement varie.
La courbe confortable
A première vue, tracer une route ne semble pas bien compliqué. On trace une ligne droite et lorsqu’un obstacle sérieux se présente, on l’évite à l’aide d’un ou plusieurs virages. Si ce procédé convenait pour des chemins empruntés par des carrosses, les routes modernes requièrent plus d’attention lors de leur tracé.
Je ne parle pas ici de relever légèrement les virages pour réduire le risque de dérapage, ni de gommer les bosses et les trous pour éviter de secouer les automobilistes et leurs passager, mais bien du tracé de la route lui même. C’est en particulier vrai pour les voies empruntées à une vitesse relativement élevée, ou les changement assez brusque de direction (typiquement les échangeurs d’autoroute).
Dans ce cas, l’approche naïve de coller une ligne droite et un arc de cercle pose un problème de confort. En effet, on passe brusquement d’une trajectoire sans courbure (la ligne droite) à une trajectoire ayant une courbure constante. Bien sûr, on peut réduire cette constante en agrandissant le virage, mais il n’empêche que pour suivre la route, le conducteur devra passer d’un seul coup d’un volant en position centrale à un volant tourné d’un certain angle. Les passagers en ressentiront nécessairement une secousse.
Pour optimiser le confort des passager, il faudrait une courbe de transition commençant avec une courbure nulle pour atteindre la courbure souhaitée du virage. Idéalement, cette courbure augmentera linéairement. La même courbe en symétrique assurera la sortie de virage.
On peut même se demander si l’arc de cercle entre les deux est vraiment nécessaire puisque la courbe pourrait augmenter sa courbure jusqu’à avoir effectué la moitié du changement de direction désiré, puis la réduire symétriquement pour la seconde moitié. Cependant, en faisant cela on risque d’atteindre une courbure élevée et donc une force centrifuge importante. Les passagers ne subiraient alors plus de secousses mais « prendraient des g » latéralement, ce qui n’est pas l’idéal pour leur confort.
A quoi ressemble donc une telle courbe ? Puisque la courbure augmente progressivement, on s’attend à retrouver une spirale. Mais quelle est sa forme exacte ?
On note t le temps écoulé depuis l’amorce du virage (le début de la courbe). La voiture roule a une vitesse constante V. On note L l’abscisse curviligne, c’est à dire la distance parcourue par la voiture depuis le début de la courbe. On a donc V = dL/dt.
Le conducteur tourne le volant progressivement avec une vitesse angulaire constante. Les roues tournent donc elles aussi avec une vitesse angulaire constante C. On note A l’angle dont à tourné la voiture depuis l’entrée de la courbe et W la vitesse angulaire de la voiture. On a donc dA/dt = W. La vitesse de rotation de la voiture augmente avec le braquage des roues. On a donc dW/dt = C = d2A/dt2.
On a donc d2A/dL2 = d2A/dt2 . dt2/dL2 = C/V. Soit en intégrant (et en prenant toutes les constantes d’intégration nulles): dA/dL = C/V.L et donc A = C/(2V).L2.
Par définition de A, cos(A) = dx/dL et sin(A) = dy/dL (ou x et y sont les coordonnées cartésiennes de la voiture dans le plan). En intégrant, on aboutit donc aux équations paramétriques suivantes:

Cette courbe est une clothoïde. Elle porte plusieurs autre nom: spirale de Cornu, spirale d’Euler, spirale de volute, spirale de transition, radioïde aux arcs … Bien sûr, la forme de la courbe n’est pas évidente à la vue de ces équations !
Heureusement, il est facile de la tracer sous wxMaxima à l’aide du code suivant:

Tracé d'une clothoïde sous wxMaxima. Pour suivre une telle courbe à vitesse constante, un automobiliste tournerait le volant avec une vitesse angulaire constante.
La courbe des sensations fortes
Un concepteur de montagnes russes va définir les caractéristiques de ses création en fonction des sensations qu’il désire faire ressentir aux futurs clients de ses attractions.
Une simple recherche sur Google Images permet de voir la variété des courbes que l’on peut trouver dans une montagne russe:
https://www.google.fr/search?q=grand+huit&tbm=isch
https://www.google.fr/search?q=montagne+russe&tbm=isch
Parmi les problèmes qu’il peut s’en poser, il y’a celui de pouvoir afficher un chiffre impressionnant. Un slogan comme « le plus haut looping du monde » apporterait à coup sûr beaucoup de clients. Mais comment faire pour atteindre des hauteurs vertigineuses ? Il y a bien sûr beaucoup de règles de conception à respecter, mais une des premières question à se poser est: quelle doit être la forme générale du looping.
Pour atteindre le haut du looping tout en ayant encore une vitesse suffisante pour être plaqué à son siège (ou au moins en apesanteur, afin de ne pas reposer de tout son poids sur les harnais), il faut une vitesse suffisante au départ de la boucle.
Avec un simple cercle, cette vitesse de départ et le rayon de courbure constant font que l’accélération subie par les passagers est très importante. On ne pourra donc pas monter très haut. Pour réduire la force subie par les passagers, il faudrait donc réduire le rayon de courbure au début de la boucle et l’augmenter progressivement jusqu’au sommet, puis le réduire à nouveau à la descente.
Bien que la clothoïde soit un bon candidat pour améliorer les loopings des montagnes russes, ce n’est pas la meilleure solution. L’idéal serait une courbe ou la force subie par les passagers, ou encore la réaction du rail sur les wagons, est constante.
La solution réside dans la quintique de l’hospital, dont les équations paramétriques sont les suivantes:


Looping d'une montagne russe: une quintique de l'Hospital approchée ? (source: Wikipedia)
Pour aller plus loin
Plus d’infomations sur le tracé d’une route:
http://fr.wikipedia.org/wiki/Tracé_en_plan_d’une_route
Force centrifuge:
http://fr.wikipedia.org/wiki/Force_centrifuge
Une collection de courbes particulières, sur Wikipedia ou sur Mathcurve:
http://fr.wikipedia.org/wiki/Courbe_brachistochrone
http://fr.wikipedia.org/wiki/Courbe_tautochrone
http://fr.wikipedia.org/wiki/Isochrone_de_Leibniz
http://fr.wikipedia.org/wiki/Clothoide
http://www.mathcurve.com/courbes2d/synchrone/synchrone.shtml
http://www.mathcurve.com/courbes2d/isochron/isochrone varignon.shtml
http://www.mathcurve.com/courbes2d/isochron/isochron.shtml
http://www.mathcurve.com/courbes2d/synodale/synodale.shtml
http://www.mathcurve.com/courbes2d/quintique de l’hospital/quintique de l’hospital.shtml
Ces courbes de base peuvent être étudiées en ajoutant des contraintes, par exemple en les plaçant sur une surface. Par exemple pour la courbe brachistochrone:
http://www.mathcurve.com/courbes3d/brachistochrone/brachistochrone.shtml
