Nous définissons notre fonction et diverses suites récurrentes l'utilisant avec des valeurs initiales différentes:
| (%i56) |
f(x):=x^2/2 - 1; u[n]:=if n=0 then 1+%i else ratsimp(f(u[n-1])); v[n]:=if n=0 then 1+2*%i else ratsimp(f(v[n-1])); w[n]:=if n=0 then 2+%i else ratsimp(f(w[n-1])); x[n]:=if n=0 then %i else ratsimp(f(x[n-1])); y[n]:=if n=0 then 0.5+0.3*%i else ratsimp(f(y[n-1])); z[n]:=if n=0 then 0.2+0.7*%i else ratsimp(f(z[n-1])); |

Pour rappel, les points de convergence de nos suites sont:
| (%i63) |
numer:false$ solve(f(x)-x); numer:true$ "Soit numériquement:"; solve(f(x)-x); |

Nous pouvons alors visualiser les différentes valeurs d'une suite:
| (%i68) |
numer:false$ for i:0 thru 10 do display(u[i]); for i:0 thru 10 do display(abs(u[i])); |

Ou plus efficace, observer graphiquement le comportement des modules, parties réelles, parties imaginaires ...
Par exemple pour 1+%i, la suite des modules converge et la suite des parties réelles aussi.
La suite des parties imaginaires alterne entre -1 et 1.
| (%i71) |
numer:false$ abs_u:makelist([n, abs(u[n])], n, 0, 20)$ real_u:makelist([n, realpart(u[n])], n, 0, 20)$ imag_u:makelist([n, imagpart(u[n])], n, 0, 20)$ wxplot2d([[discrete, abs_u], [discrete, real_u], [discrete, imag_u]], [style, points], [y,-1.5,2.5], [legend, "module", "reelle", "imaginaire"])$ |

Notez l'échelle logarithmique pour les deux graphiques qui suivent.
La divergence est flagrante.
| (%i76) |
numer:false$ abs_v:makelist([n, abs(v[n])], n, 0, 8)$ real_v:makelist([n, realpart(v[n])], n, 0, 8)$ imag_v:makelist([n, imagpart(v[n])], n, 0, 8)$ wxplot2d([[discrete, abs_v], [discrete, real_v], [discrete, imag_v]], [style, points], [logy], [legend, "module", "reelle", "imaginaire"])$ |
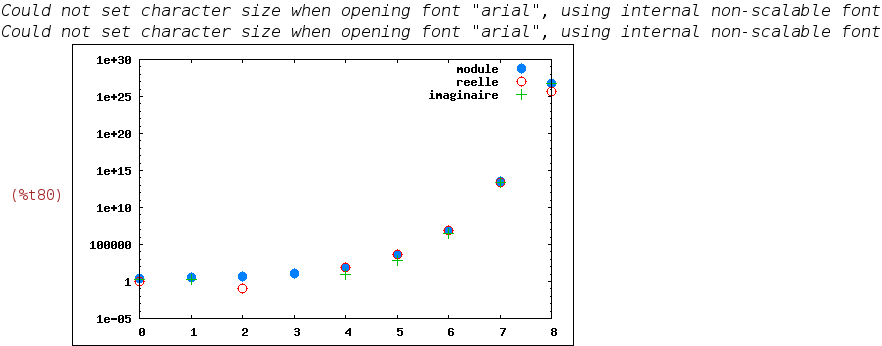
On notera l'alternance des parties réelles et imaginaires.
| (%i81) |
numer:true$ abs_w:makelist([n, abs(w[n])], n, 0, 8)$ real_w:makelist([n, realpart(w[n])], n, 0, 8)$ imag_w:makelist([n, imagpart(w[n])], n, 0, 8)$ wxplot2d([[discrete, abs_w], [discrete, real_w], [discrete, imag_w]], [style, points], [logy], [legend, "module", "reelle", "imaginaire"])$ "Parties réelles:";real_w; "Parties imaginaires:";imag_w; |

| (%i90) |
numer:true$ abs_x:makelist([n, abs(x[n])], n, 0, 20)$ real_x:makelist([n, realpart(x[n])], n, 0, 20)$ imag_x:makelist([n, imagpart(x[n])], n, 0, 20)$ wxplot2d([[discrete, abs_x], [discrete, real_x], [discrete, imag_x]], [style, points], [legend, "module", "reelle", "imaginaire"])$ "La suite est réelle et converge vers:"; x[100]; |

Maxima ne parvient pas à calculer les modules au delà du 7ème élement.
Pourtant, la suite converge.
| (%i97) |
numer:true$ abs_y:makelist([n, abs(y[n])], n, 0, 7)$ real_y:makelist([n, realpart(y[n])], n, 0, 20)$ imag_y:makelist([n, imagpart(y[n])], n, 0, 20)$ wxplot2d([[discrete, abs_y], [discrete, real_y], [discrete, imag_y]], [style, points], [legend, "module", "reelle", "imaginaire"])$ "La suite converge vers: ";y[100]; |

Ici encore, maxima ne parvient pas à calculer le module pour un rang supérieur à 6.
Mais la suite converge bien.
| (%i104) |
numer:true$ abs_z:makelist([n, abs(z[n])], n, 0, 6)$ real_z:makelist([n, realpart(z[n])], n, 0, 100)$ imag_z:makelist([n, imagpart(z[n])], n, 0, 100)$ wxplot2d([[discrete, abs_z], [discrete, real_z], [discrete, imag_z]], [style, points], [legend, "module", "reelle", "imaginaire"])$ "La suite converge vers";z[100]; |
