Etude générique de la trajectoire

Étudions la trajectoire d’un projectile de vitesse initiale v = 100 m/s et soumis à l’accélération de la pesanteur g = 9.81 m/s².
L’absisse et l’ordonnée du projectile lancé depuis l’origine (0, 0) dans une direction faisant un angle a avec l’horizontale sont:

(%i1)

Y(t) := -g/2*t^2+v*sin(a)*t; X(t) := v*cos(a)*t;

L’ordonnée en un point x est donc:

(%i3)

y(x, a) := Y(x/(v*cos(a)))$ y = y(x, a);

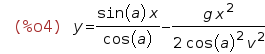
Numériquement et graphiquement, pour un angle de 0.5 radians (environ 28.6°):

(%i5)

f(g, v, a) := y(x, a)$ ynum(x, a) := f(9.81, 100, a)$ y = ynum(x, 0.5); wxplot2d([ynum(x, 0.5)], [x, 0, 900], [y, 0, 150])$

L’ensemble des trajectoires pour un intervalle de valeur de l’angle a peut être dessiné sous forme d’une courbe en 3D:

(%i9)

plot3d(ynum, [x, 0, 1000], [a, 0, 1], [elevation, 90], [azimuth, 0])$ wxplot3d(ynum, [x, 0, 1000], [a, 0, 1], [elevation, 90], [azimuth, 0])$

Recherche de la portée maximale

Un point au sol (y = 0) peut être atteint pour un x donné en choisissant a tel que:

(%i11)

solve(y(x, a), x);

La solution générale x = 0 correspond au point de départ. La solution qui nous intéresse pour la recherche de la portée maximale est donc:

(%i12)

solve(y(x, a), x)$ define(x_max(a), trigreduce(rhs(%[1])));

Qui est maximale pour (condition nécessaire mais non suffisante):

(%i14)

solve(diff(x_max(a), a, 1), a);

On vérifie effectivement que pi/4 est solution. D’ailleurs la dérivée seconde en ce point est négative:

(%i15)

d2x_max(a) := diff(x_max(a), a, 2)$ ‘at(‘diff(x_max(a), a, 2), [a = pi/4]) = at(d2x_max(a), [a = %pi/4]), numer;

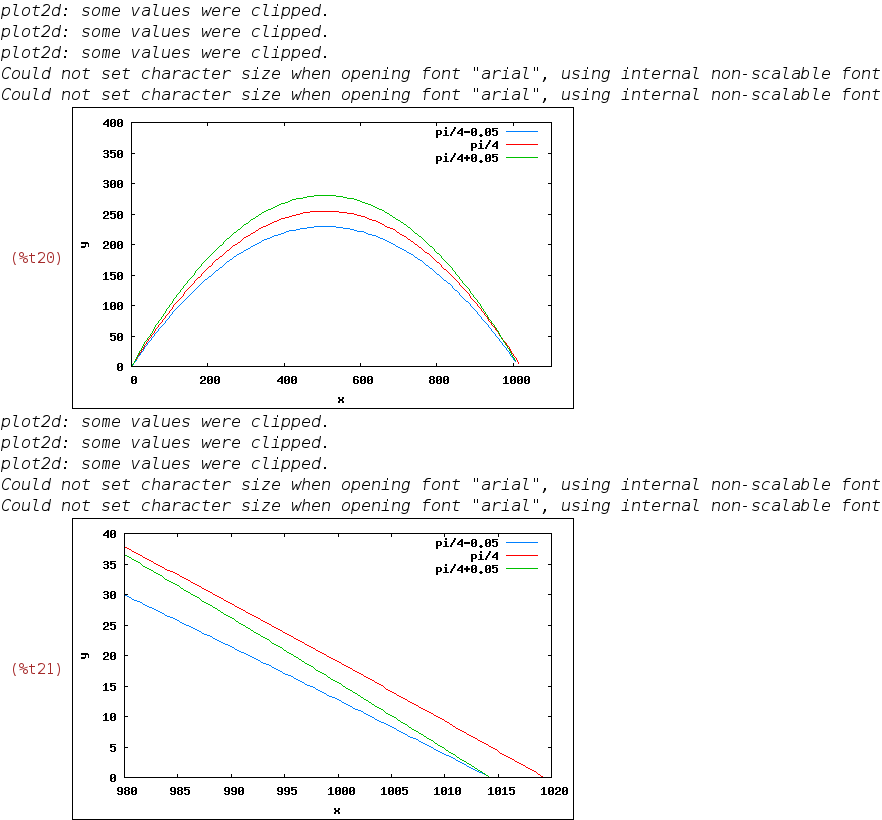
On vérifie graphiquement que pour des angles légèrement inférieurs ou supérieurs à pi/4, le projectile termine sa course moins loins que pour un angle égal à pi/4:

(%i17)

yd1(x) := f(9.81, 100, %pi/4 – 0.05)$ yd2(x) := f(9.81, 100, %pi/4)$ yd3(x) := f(9.81, 100, %pi/4 + 0.05)$ wxplot2d([yd1(x), yd2(x), yd3(x)], [x, 0, 1100], [y, 0, 400], [legend, pi/4-0.05, pi/4, pi/4+0.05])$ wxplot2d([yd1(x), yd2(x), yd3(x)], [x, 980, 1020], [y, 0, 40], [legend, pi/4-0.05, pi/4, pi/4+0.05])$

Recherche du lieu des hauts de trajectoire

Le projectile atteint le haut de sa trajectoire lorsque y est à son maximum, ce qui peut se produire uniquement si dy/dx = 0 (condition nécessaire mais non suffisante).
On en déduit l’absisse du haut de la trajectoire en fonction de l’angle a.

(%i22)

‘diff(‘y(x,a), x, 1) = diff(y(x,a), x, 1); solve([diff(y(x,a), x, 1)], [x])$ define(x_haut(a), rhs(%[1]))$ x = x_haut(a); y = y(x_haut(a), a);

On peut tracer le lieu des hauts de trajectoire:

(%i27)

xh(g, v) := x_haut(a)$ yh(g, v) := y(x_haut(a), a)$ wxplot2d([[‘parametric, xh(9.81, 100), yh(9.81, 100), [a, 0.01, 3.2], [nticks, 300]]], [x,-1000,1000], [y,0,800])$

Recherche de la zone de sûreté

La zone de sûreté est la zone constituée des points que le projectile ne peut pas atteindre quelque soit l’angle a.
Elle est délimitée par la courbe des ordonnées maximales pouvant être atteintes pour chaque valeur d’absisse.
Pour une valeur de x donnée, l’ordonnée maximale est atteinte pour a tel que dy/da = 0:

(%i30)

dy_da(x) := diff(y(x,a),a,1)$ ‘diff(‘y(x,a), a, 1) = dy_da(x); solve(dy_da(x), x); define(xs(a), trigsimp(rhs(%[1]))); ys(a) := y(xs(a), a)$ ‘ys(a) = ys(a); xs_num(g, v) := xs(a)$ ys_num(g, v) := ys(a)$ wxplot2d([[‘parametric, xs_num(9.81, 100), ys_num(9.81, 100), [a, 0.01, 3.2], [nticks, 300]]], [x,-1200,1200], [y,0,600])$

L’équation cartésienne de la courbe peut être obtenue facilement:

(%i39)

solve(x=trigreduce(xs(a)), a); y = ratexpand(ys(rhs(%[1])));

---

Created with wxMaxima.