 Il est minuit à Londres et le White Horse, pub populaire du quartier de Soho ferme ses portes. John, le propriétaire pousse dehors le dernier client, un habitué, et ferme la porte à clef derrière lui. De derrière la vitre, il l’observe remonter Rupert Street en titubant. Trébuchant sur un pavé, il tourne légèrement vers la gauche, traverse la rue puis, faisant face à un lampadaire, prend appui dessus pour faire un quart de tour et repartir sur la droite avant de s’engouffrer dans Shaftesbury Avenue.
Il est minuit à Londres et le White Horse, pub populaire du quartier de Soho ferme ses portes. John, le propriétaire pousse dehors le dernier client, un habitué, et ferme la porte à clef derrière lui. De derrière la vitre, il l’observe remonter Rupert Street en titubant. Trébuchant sur un pavé, il tourne légèrement vers la gauche, traverse la rue puis, faisant face à un lampadaire, prend appui dessus pour faire un quart de tour et repartir sur la droite avant de s’engouffrer dans Shaftesbury Avenue.
Depuis 10 ans qu’il le chasse tous les jours à l’heure de la fermeture, John a vu cet ivrogne prendre toutes les directions possibles à la sortie du pub. Il l’a même déjà vu repasser devant le bar plus tard, alors qu’il était en train de nettoyer. Parfois dans le sens inverse, mais aussi dans le même sens !
Alors qu’il commence à passer le balai, John observe la poussière sous les lumières blafardes et se dit que l’ivrogne est un peu pareil à ces grains ballottés par les courants d’air, changeants de direction de manière erratique. Puis ses yeux se posent sur le tabouret où était installé l’ivrogne une dizaine de minute plus tôt et à son pied, il aperçoit une sacoche oubliée par son fidèle client. Fouillant à l’intérieur, il y trouve non seulement son porte-feuille, mais aussi ses clefs.
Réalisant qu’il faudra sans doute plusieurs heures à l’ivrogne pour retrouver son domicile, puis à nouveau plusieurs heures pour revenir de son domicile au bar, il se dit qu’il doit y’avoir un moyen d’éviter d’être réveillé à l’aube par un soûlard à la recherche de son trousseau de clefs. Si seulement il n’habitait pas juste au dessus de son bar, il n’aurait pas de tels problèmes !
Mais l’ivrogne est parti il y a bien 10 minutes. Quel chance a-t-il de le retrouver ?
La marche aléatoire
Une marche aléatoire est une dynamique discrète composée d’une succession de pas aléatoires totalement décorrélés les uns des autres. À chaque instant, les positions à venir dépendent de l’état présent, mais pas de l’état passé. L’étude mathématique des marches aléatoires à de nombreuses applications en physique en informatique et en économie. La marche de notre ivrogne peut être modélisée par une marche aléatoire de plusieurs manières.

Marche aléatoire discrète isotrope à deux dimensions sur un réseau régulier. La taille de pas est de un pixel, contrairement au programme qui suis où la taille de pas est réglée à 5 pixels.
Si notre ivrogne choisit aléatoirement sa direction à chaque carrefour, puis suis la rue jusqu’au carrefour suivant, alors nous avons une marche aléatoire discrète isotrope à deux dimensions sur un réseau irrégulier. Discrète car l’ivrogne avance d’un carrefour à un autre adjacent à chaque étape de la marche, sa progression n’est pas continue (dans le modèle). Isotrope car lors de ses choix, l’ivrogne ne favorise aucune des directions possibles. À deux dimensions car l’ivrogne évolue dans les rues de Londres que l’on peut ramener à un plan (dans le sens mathématique). Sur un réseau irrégulier car le plan de Londres n’est pas un simple quadrillage de rue, c’est un graphe complexe. Certains carrefours ont 3 rues, d’autres 4 ou plus.
Si notre ivrogne arrive sur une grande place plate sans obstacle et titube, sa marche devient une marche aléatoire continue isotrope à deux dimensions. Continue car l’ivrogne peut faire des pas plus ou moins grand. La taille des pas est choisie aléatoirement dans un ensemble continu. Si tous ses pas faisaient la même taille, la marche serait discrète mais sur un réseau régulier, car quel que soit l’endroit où se trouve l’ivrogne, les mêmes déplacements sont possibles.
Enfin, si l’on prend en compte le relief, notre ivrogne aura sans doute tendance a préférer prendre les rues qui descendent que les rues qui monte. Sur une place en pente, il fera sans doute des pas plus grands dans le sens de la descente que dans celui de la montée. La marche est alors anisotrope.
Programmer la marche aléatoire
Nous l’avons vu, il existe de nombreux types de marches aléatoires. Dans tous les cas, il s’agit de déplacer un point dans un espace en ne se souciant que de sa position actuelle pour déterminer sa position à venir. Avant de se lancer dans un programme modélisant une marche donnée, on peut se demander si il serait possible de lui faire supporter plusieurs types de marches:
- Dans des espaces à plus de deux dimensions (ou même dans un espace à une dimension). Cela signifie simplement utiliser des points ayant un nombre de coordonnées égales au nombre de dimensions, et gérer le déplacement selon tous les axes.
- Anisotrope: cela est plus complexe car il faut définir l’anisotropie. La manière la plus générale de gérer l’anisotropie est de définir une fonction fournissant pour chaque point une probabilité pour chaque direction.
- Réseau régulier ou irrégulier. Supporter la définition d’un réseau est le plus gros développement par rapport à une implémentation naïve sur
 . Mais techniquement, une fois que l’on supporte la marche aléatoire sur un graphe, alors le nombre de dimensions de la marche n’est qu’une question d’affichage, pas de logique. Et la définition de l’anisotropie peut être inclue dans le graphe en donnant un poids à chaque arc, avec en plus la possibilité d’avoir des poids différents selon le sens de parcours de l’arc et des arcs à sens unique.
. Mais techniquement, une fois que l’on supporte la marche aléatoire sur un graphe, alors le nombre de dimensions de la marche n’est qu’une question d’affichage, pas de logique. Et la définition de l’anisotropie peut être inclue dans le graphe en donnant un poids à chaque arc, avec en plus la possibilité d’avoir des poids différents selon le sens de parcours de l’arc et des arcs à sens unique.
À noter que le réseau irrégulier étant irrégulier, il doit être défini exhaustivement et sera donc fini, à moins d’être généré de manière aléatoire. Mais le réseau régulier lui, peut être infini dans la mesure ou il suffit de définir un motif qui se répète.
Implementation simple
Voilà l’implémentation simple, en python et utilisant pygame pour l’affichage, d’une marche aléatoire discrète isotrope à deux dimensions sur  . Le contrôle se fait à l’aide des touches suivantes:
. Le contrôle se fait à l’aide des touches suivantes:
- Echap pour quitter
- C pour afficher la courbe de la distance (à vol d’oiseau) du marcheur par rapport à son point de départ tout au long de sa course
- P pour revenir à la vue en plan de la marche aléatoire
- R pour réinitialiser le programme
- N pour ajouter un marcheur
- F pour accélérer la marche
- S pour ralentir la marche

Distance parcourue par 6 marcheurs aléatoires après 100 000 pas. L'axe Y représente une distance en pas, l'axe allant jusqu'à un peu plus de 500. En 100 000 pas, aucun des 6 marcheurs ne s'est éloigné de plus de 350 pas à vol d'oiseau de son point de départ.
Du point de vue des performances, on remarquera que c’est la génération des nombres aléatoires qui prend la majeure partie du temps.
Mathématiquement
Plaçons notre ivrogne dans un couloir, il ne peut que faire des pas en avant ou en arrière. Nous obtenons la version la plus simple de marche aléatoire: la marche aléatoire discrète isotrope à une dimension. Elle peut être observée facilement avec le programme ci-dessus en n’affectant jamais aucune valeur à dy, seulement à dx. La vue plan n’est alors pas très intéressante, mais la vue courbe permet d’observer l’éloignement par rapport à l’origine.

Distance parcourue par 6 marcheurs aléatoires après 100 000 pas. Dans une marche aléatoire à 1 dimension, le retour à l'origine est courant, dans la mesure où c'est un passage obligatoire avant d'atteindre l'autre côté ... La distance maximale ne semble pas différer beaucoup du cas à 2 dimensions.
A chaque étape, le marcheur peut soit avancer d’un pas, soit reculer d’un pas. La probabilité de chaque événement est de 1/2. La position du marcheur se résume à la coordonnée x qui est la somme des choix, 1 correspondant à avancer et -1 à reculer.
Chaque étape est une épreuve de Bernouilli. La probabilité d’avoir effectué k pas en avant (et donc n-k pas en arrière) après n pas est:
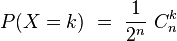
Dans ce cas, le marcheur se trouve à une distance k-(n-k)=2k-n de l’origine. À noter que, étant donnée la symétrie du problème, c’est aussi la probabilité de se trouver à (n-k)-k=n-2k pas de l’origine.
L’espérance est nulle. En lançant un grand nombre de marcheurs, le nuage de leurs positions sera plus ou moins centré sur leur point de départ. Mais si l’on étudie la distance du marcheur par rapport à son point de départ, c’est à dire l’espérance de la valeur absolue, on obtient une moyenne de  . En 1756, de Moivre montre que la moyenne est proportionnelle à
. En 1756, de Moivre montre que la moyenne est proportionnelle à  que les pas soient de taille fixes ou aléatoires, quel que soit le nombre de dimensions et même si le marcheur peut choisir aléatoirement sa direction de manière homogène. Seule la constante de proportionnalité dépend des conditions.
que les pas soient de taille fixes ou aléatoires, quel que soit le nombre de dimensions et même si le marcheur peut choisir aléatoirement sa direction de manière homogène. Seule la constante de proportionnalité dépend des conditions.

Evolution de la distance à leur point d'origine de 8 marcheurs (en bleus et verts), moyenne des 8 distances (en rouge) et moyenne théorique (en blanc)
De plus, la loi binomiale se comportant asymptotiquement comme la loi normale (théorème de la limite centrale), on s’attend à ce que 95% des marcheurs soient à moins de 2 pas de leur point de départ après n pas. Ces résultats aussi sont transposables aux cas à dimensions supérieures.
pas de leur point de départ après n pas. Ces résultats aussi sont transposables aux cas à dimensions supérieures.
Une différence apparaît cependant avec l’augmentation des dimensions: les chances de repasser par l’origine réduisent au fur et à mesure que le nombre de dimensions augmente. Le théorème de Polya montre que:
- pour les cas à 1 et 2 dimensions, sur une durée infinie, le marcheur repassera un nombre infini de fois par son point de départ
- pour les cas à plus de 3 dimensions, le marcheur ne repassera qu’exceptionnellement à son point de départ.
D’une manière plus générale, la probabilité pour le marcheur de se retrouver à son point de départ à l’étape 2n (le retour ne peut pas se faire à une étape impaire) est en O(n-d/2) quand n devient grand.
Revenons en à John
Quelle leçon John peut-il tirer de tout cela ? On remarque que si l’ivrogne est parti il y a moins de 10 minutes, il y a de fortes chances qu’il soit dans un rayon assez faible autour du bar. En faisant le tour du pâté de maison, John pourrait bien apercevoir son client et sauver sa grasse matinée. Et, si certaines rues du quartier sont en pentes, il a tout intérêt à aller chercher en bas de celles-ci !
Un peu plus de marcheurs
Lançons maintenant des marcheurs aléatoires (un pixel) depuis un coin de l’écran et laissons les errer librement dans un plan contenant seulement quelques greffons (un ou plusieurs pixels). Lorsque un marcheur se heurte à un greffon ou un marcheur déjà accroché, il s’y accroche et reste à cette position. Un autre marcheur est alors lancé.

Marcheurs aléatoires s'accrochant à un "greffon" central. Afin de visualiser la progression de l'agrégat, les premiers marcheurs sont rouges. Les suivants virent progressivement au vert, puis au bleu, puis au rouge et recommencent.
Le comportement observé peut être retrouvé dans des domaines variés, à quelques ajustements prêts:
- La formation de flocons de neige par agrégation de micro-gouttes d’eau en suspension dans l’air
- La formation par calcification des arborescences coralliennes
- Les motifs de drainage dûs à l’érosion
- Les croissances denditriques
- …
L’ajout d’une contrainte dans le déplacement aléatoire permet de simuler d’autres phénomènes. Par exemple, en favorisant une direction dans le déplacement aléatoire, on obtiendra une simulation de la gravité permettant de modéliser un dépôt de poussière ou de la sédimentation.

Dendrites formées suite à une sédimentation
Pour en savoir plus
Une expérience grandeur réelle s’est déroulée à Toulouse en 2005: http://mappemonde.mgm.fr/actualites/M_toulouse2.html
Démonstrations du théorème de Polya: http://www.proba.jussieu.fr/pageperso/eric/polya.pdf
Notes de cours et TD « Introduction à la physique numérique » de l’université de Montreal:
http://www.astro.umontreal.ca/~paulchar/phy1234/notes/notes13.pdf
http://www.astro.umontreal.ca/~paulchar/phy1234/labos/lab9www.pdf
Wikipedia bien sûr:
http://fr.wikipedia.org/wiki/Marche_aléatoire http://fr.wikipedia.org/wiki/Loi_de_Bernoulli http://fr.wikipedia.org/wiki/Théorème_central_limite
